Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 64

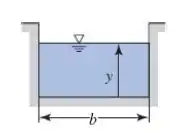
Uma calha retangular acima do solo retangular está para ser construída em madeira. Para uma queda de 1,9 m/km, qual será a profundidade e largura para a calha mais econômica se ela tiver que descarregar 1,1 m³/s?

Passo 1

Beleza! Sabemos que a equação da descarga para o sistema é dada por:

Q = 1 n A R h 2 3 S b 1 2

Com o auxílio da tabela de geometria fornecida nessa seção, temos:

A = b y

R h = b y b + 2 y

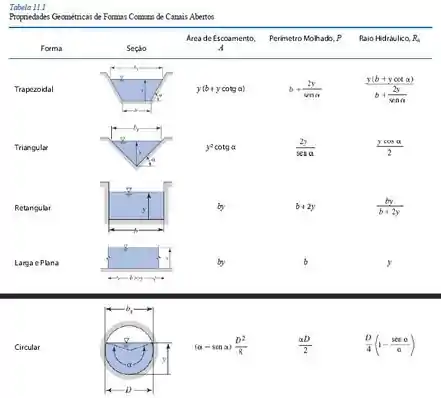
E, agora, vamos recorrer à tabela 11.3 que fornece a geometria ótima para cada canal, então:

b = 2 y n = 2 y

Passo 2

Agora, para encontrar o coeficiente de rugosidade de Manning, vamos checar a tabela fornecida nessa seção do livro:

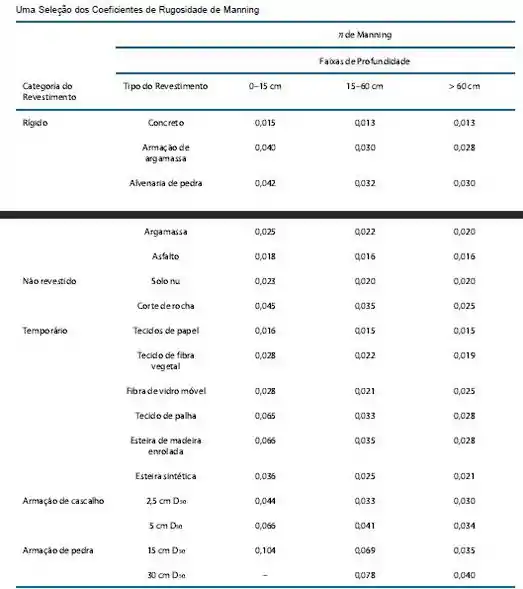
Infelizmente não temos um revestimento de madeira na tabela, então, pesquisando esse valor na internet, podemos adotar:

n = 0,013

Então, agora, vamos utilizar o valor de b ótimo encontrado no passo 1 e substituir esse valor na expressão para a área e para o raio hidráulico:

A = b y = 2 y ( y ) → A = 2 y 2

R h = b y b + 2 y = 2 y ( y ) 2 y + 2 y = 2 y 2 4 y → R h = y 2

Passo 3

Então, substituindo os valores conhecidos na equação de descarga, temos:

Q = 1 n A R h 2 3 S b 1 2 → 1,1 = 1 0,015 ( 2 y 2 ) y 2 2 3 1,9 1000 1 2

0,3 = y 2 y 2 3 → 0,3 = y 8 / 3 → 0,3 3 8 = y → y = 0,637   m

Então, substituindo esse valor na expressão para a largura do canal, temos:

b = 2 y = 2 0,637 → b = 1,274   m

Resposta

y = 0,637   m

b = 1,274   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a profundidade crítica para o canal no Problema 11.41. (Correção: o enunciado na verdade se refere ao Problema 11.42, o 11.41 não é um canal e nem faz parte dos problemas de escoamento uniform
Mostre que a melhor seção trapezoidal hidráulica é a metade de um hexágono.
Um canal retangular com 3m de largura carrega 2,83m 3 / s sobre um fundo horizontal a uma profundidade de 0,3m . Um ressalto suave através do canal está a 10c m acima do fundo. Determine a elevação da
Um canal retangular com 3m de largura carrega 0,57m 3 / s a uma profundidade de 0,27m . Um ressalto suave através do canal está a 0,06m acima do fundo do canal. Estime a variação local na profundidade
Para o canal do problema FE10.1, a profundidade da água mais eficiente (maior vazão para uma dada declividade e resistência) é(a) 1 m, (b) 1,5 m, (c) 2 m, (d) 2,5 m, (e) 3 m