Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 61
Mostre que a melhor seção trapezoidal hidráulica é a metade de um hexágono.
Passo 1
Tá legal, para fazer essa demonstração vamos precisar nos lembrar um pouco de geometria. Sabemos que a fórmula para o ângulo interno de um polígono é:
Então, para um hexágono, com , temos:
Então, olhando para a ilustração do canal trapezoidal do enunciado, temos que nosso terá que ser igual a:
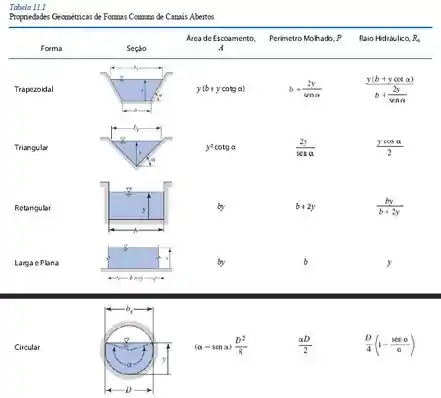
Então vamos lá! Com o auxílio da tabela de geometria fornecida nessa seção, temos:
Passo 2
Tá legal! Aqui vamos isolar da equação da área e substituir na do perímetro molhado, então, temos:
Então, substituindo na do perímetro molhado:
Agora, para obtermos a seção transversal da eficiência hidráulica ótima, vamos derivar a expressão anterior em relação à e depois igualar o resultado a zero para maximizar a eficiência em função de . Então, temos:
Para as condições ótimas então, devemos ter:
Então, substituindo esses valores na equação anterior, temos:
Passo 3
Agora precisamoa maximizar a área em função de , então vamos derivar a função encontrada no passo 2 para a área em função de e depois igualar ela a zero, então, temos:
Nesse caso, podemos dividir toda a equação por , então, temos:
Multiplicando os dois lados da equação por , temos:
No entanto, sabemos da relação fundamental da trigonometria que , então, teremos:
Opa! Conseguimos chegar na demonstração que precisávamos!
Resposta
Ei, a resposta está no passo a passo :)