Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 82

Uma camada de água, com 2   m m de espessura, sobre uma placa eletricamente aquecida é mantida a uma temperatura de T a = 340   K , enquanto ar seco a T ∞ = 300   K escoa sobre a sua superfície (caso A). O conjunto é circundado por uma grande vizinhança que também está a 300   K .

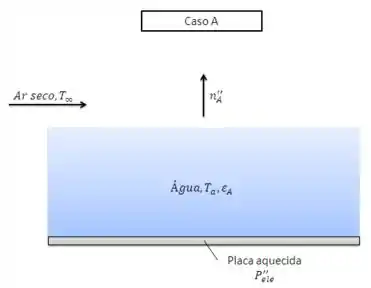
(a) Se o fluxo de evaporação na superfície da água para o ar for de n A ' ' = 0,030   k g / s m 2 , qual é o valor correspondente do coeficiente de transferência de massa por convecção? Quanto tempo levará para a água evaporar completamente?

(b) Quais são os valores correspondentes do coeficiente de transferência de calor por convecção e da taxa na qual a potência elétrica deve ser fornecida, por unidade de área da placa, para manter a temperatura especificada da água? A emissividade da água é ε a = 0,95 .

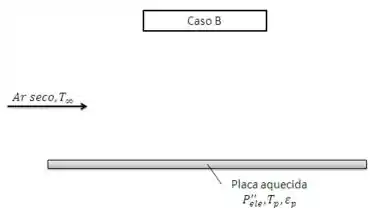
(c) Se a potência elétrica determinada na parte (b) for mantida após a completa evaporação da água (caso B), qual é a temperatura resultante da placa, cuja emissividade é ε p = 0,60 ?

Passo 1

O item (a) nos pede para encontrar o coeficiente de transferência de massa. Sabemos que o ar está seco ( ρ A , ∞ = 0 ) e que a água está a uma temperatura T a = 340   K . Nesta temperatura:

v ^ A = 5,74   m 3 / k g

De acordo com a tabela A - 6 , apêndice A do livro. A partir destes dados podemos aplicar a equação de fluxo de massa:

n A ' ' = h - m ( ρ A , s - ρ A , ∞ )

n A ' ' = h - m ( 1 / v ^ A - 0 )

0,030 = h - m ( 1 / 5,74 - 0 )

h - m = 0,030 × 5,74

h - m = 0,172   m / s

Neste item também precisamos determinar o tempo para evporar o filme de água de espessura L = 2 × 10 - 3   m . Para isso, vamos considerar que o fluxo se mantém constante durante todo o processo de evaporação e, aplicaremos a seguinte relação:

n A ' ' = m A A t

n A ' ' = ρ V A t

n A ' ' = ρ A L A t

n A ' ' = ρ L t

t = ρ L n A ' '

A densidade da água líquida na temperatura de T a = 340   K é:

ρ = 1 1,021 × 10 - 3

ρ = 979,43   k g / m 3

Ficamos então com:

t = 979,43 × 2 × 10 - 3 0,030

t = 65,3   s

Passo 2

Para o item (b) precisamos começar determinando o coeficiente de transferência de calor. Para isso, vamos aplicar a analogia de Reynolds:

h h m = ρ c p L e 2 / 3

Mas antes, precisamos determinar as propriedades do ar na temperatura de filme. A temperatura de filme é:

T f = T s + T ∞ 2

T f = 300 + 340 2 = 640 2

T f = 320   K = 4 7 ° C

Pelas tabelas A-4 e A-8 do apêndice A:

k = 0,028   W / m K

ρ = 1,08   k g / m 3

c p = 1008   J / k g K

D A B ( 298   K ) = 0,26 × 10 - 4   m 2 / s

Nosso próximo passo será obter a difusividade para a temperatura de filme através da relação:

D A B 1 D A B 2 = T 1 T 2 3 / 2

D A B 2 = D A B 1 T 2 T 1 3 / 2

D A B 2 = 0,26 × 10 - 4 × 320 298 3 / 2

D A B 2 = 0,29 × 10 - 4   m 2 / s

Passo 3

Continuando o item (b), vamos agora calcular o número de Lewis:

L e = k ρ c p D A B

L e = 0,028 1,08 × 1008 × 0,29 × 10 - 4

L e = 0,889

Aplicando na analogia de Reynolds:

h = h m ρ c p L e 2 / 3

h = 0,172 × 1,08 × 1008 × 0,889 2 / 3

h = 173,1   W / m 2 K

Devemos agora determinar qual é a potência fornecida pela placa. Para isso, vamos considerar que o sistema está em regime estacionário e que não há geração de energia. Além disso, o sistema perde energia por convecção, radiação e evaporação. O balanço de energia para o sistema fica:

d E d t = E ˙ e n t - E ˙ s a í d a + E ˙ g e r

0 = E ˙ e n t - E ˙ s a í d a + 0

0 = P e l e ' ' - ( q c o n v ' ' + q e v ' ' + q r a d ' ' )

P e l e ' ' = q c o n v ' ' + q e v ' ' + q r a d ' '

Precisamos então determinar o fluxo de calor perdido por cada mecanismo.

Começando com convecção:

q c o n v ' ' = h ( T s - T ∞ )

q c o n v ' ' = 173,1 × ( 340 - 300 )

q c o n v ' ' = 6924,78   W / m 2

O próximo é radiação:

q r a d ' ' = ε σ T s 4 - T ∞ 4

q r a d ' ' = 0,95 × 5,67 × 10 - 8 × 340 4 - 300 4

q r a d ' ' = 283,51   W

Por fim, o fluxo de calor perdido por evaporação:

q e v ' ' = n A ' ' ∆ H e v

Pela tabela A-6 do apêndice A, para T a = 340   K :

∆ H e v = 2342000   J / k g

Então:

q e v ' ' = 0,03 × 2342000

q e v ' ' = 70260   W / m 2

A potência por área necessária é:

P e l e ' ' = 6924,78 + 70260 + 283,51

P e l e ' ' = 77468,3   W / m 2

Passo 4

Vamos agora para o item (c). Considerando que não há mais água devemos obter a temperatura da placa. Para este caso, teremos transferência de calor por convecção e radiação. O balanço de energia fica:

d E d t = E ˙ e n t - E ˙ s a í d a + E ˙ g e r

0 = E ˙ e n t - E ˙ s a í d a + 0

0 = P e l e ' ' - ( q c o n v ' ' + q r a d ' ' )

P e l e ' ' = q c o n v ' ' + q r a d ' '

Devemos então, aplicar as novas relações para cada fluxo de calor:

P e l e ' ' = h ( T p - T ∞ ) + ε σ T p 4 - T ∞ 4

77468,3 = 173,1 × ( T p - 300 ) + 0,6 × 5,67 × 10 - 8 × T p 4 - 300 4

Com auxílio de Excel ou outro programa de cálculo podemos encontrar o valor de T p que satisfaz a equação. Então,

T p = 701,5   K = 428,5 ° C

Resposta

(a) h - m = 0,172   m / s

t = 65,3   s .

(b) h = 173,1   W / m 2 K

P e l e ' ' = 77468,3   W / m 2 .

(c) T p = 701,5   K = 428,5 ° C .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco com 20m m de diâmetro está coberto por uma película de água. Sob condições de regime estacionário, um aquecedor com potência de 200m W é necessário para manter o sistema disco-película de águ
Um processo industrial envolve a evaporação de uma fina película de água sobre uma superfície curva, através do seu aquecimento pela sua parte inferior e pelo escoamento forçado de ar na parte superio
Deseja-se desenvolver um modelo simples para prever o histórico temperatura-tempo de uma placa durante o ciclo de secagem em uma máquina de lavar louças. Após o ciclo de lavagem, a placa encontra-se a
Um experimento é conduzido para determinar o coeficiente de transferência de massa por convecção médio em uma pequena gota usando um aquecedor controlado para operar a uma temperatura constante. O his