Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 84

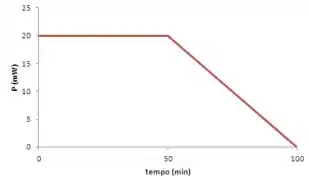
Um experimento é conduzido para determinar o coeficiente de transferência de massa por convecção médio em uma pequena gota usando um aquecedor controlado para operar a uma temperatura constante. O histórico da potência requerida para evaporar completamente a gota a uma temperatura de 37 ° C é mostrado na figura. Foi observado que, à medida que a gota seca, o seu diâmetro molhado sobre a superfície do aquecedor permanece praticamente constante em um valor de 4   m m .

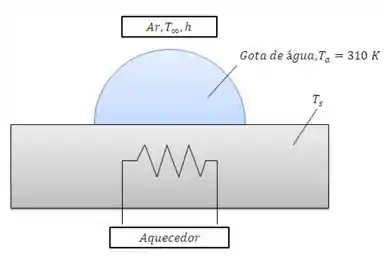
(a) Calcule o coeficiente de transferência de massa por convecção médio baseado na área molhada durante o processo de evaporação, para condições nas quais a gota, o aquecedor e o ar ambiente seco estão a 37 ° C .

(b) Quanta energia será necessária para evaporar a gota se a temperatura do ar ambiente seco for de 27 ° C , enquanto a temperatura do sistema gota-aquecedor se mantém em 37 ° C ?

Passo 1

O item (a) nos pede para determinar o coeficiente de transferência de massa para a condição em que T s = T a = T ∞ = 37 ° C . Vamos começar aplicando o balanço de energia em regime permanente, considerando que não há geração de energia:

d E d t = E ˙ e n t - E ˙ s a í d a + E ˙ g e r

0 = E ˙ e n t - E ˙ s a í d a

E ˙ e n t = E ˙ s a í d a

Para este caso temos o aquecedor fornecendo energia e perda apenas por evaporação, já que T a - T ∞ = 0 . Então:

P = q e v

∫ 0 t f P d t = Q e v

A integral é a área abaixo da curva P × t , então:

20 × 10 - 3 × 50 × 60 + 20 × 10 - 3 × ( 100 - 50 ) × 60 2 = Q e v

Q e v = 90   J

A perda de calor por evaporação é:

Q = M ∆ H e v

Em que

∆ H e v = 2414000   J / k g

De acordo com a tabela A-6, para água a T a = 310   K .

Então:

90 = M × 2414000

M = 90 2414000

M = 3,728 × 10 - 5   k g

Passo 2

A massa evaporada pode ser expressa como:

M = m ˙ t

Então, a vazão mássica de água é:

m ˙ = M t

Alternativamente, podemos escrever

m ˙ = h - m A ρ A , s - ρ A , ∞

Juntando as equações:

M t = h - m A ρ A , s - ρ A , ∞

Considerando que o ar está seco ρ A , ∞ = 0 e buscando o valor da densidade ρ A , s para T a = 310   K :

3,728 × 10 - 5 100 × 60 = h - m π D 2 4 0,04361 - 0

h - m = 3,728 × 10 - 5 × 4 100 × 60 × 0,04361 × π D 2

h - m = 0,0113   m / s

Passo 3

Vamos agora determinar a energia necessária para manter as condições do sistema, considerando agora que T ∞ = 300   K . Para este caso, teremos a adição da perda de energia por convecção. Nosso balanço de energia será:

d E d t = E ˙ e n t - E ˙ s a í d a + E ˙ g e r

0 = E ˙ e n t - E ˙ s a í d a

E ˙ e n t = E ˙ s a í d a

Q = Q e v + Q c o n v

A perda de calor por convecção é dada por:

Q c o n v = h - A T s - T ∞ t

Precisamos então do coeficiente convectivo de transferência de calor. Para obtê-lo vamos aplicar a analogia termo-mássica:

h - h - m = ρ c p L e 2 / 3

Mas antes, precisamos determinar as propriedades do ar na temperatura de filme. A temperatura de filme é:

T f = T s + T ∞ 2

T f = 310 + 30 0 2 = 6 1 0 2

T f = 305   K = 32 ° C

Pelas tabelas A-4 e A-8 do apêndice A:

k = 0,02667   W / m K

ρ = 1,1448   k g / m 3

c p = 1007,2   J / k g K

D A B ( 298   K ) = 0,26 × 10 - 4   m 2 / s

Nosso próximo passo será obter a difusividade para a temperatura de filme através da relação:

D A B 1 D A B 2 = T 1 T 2 3 / 2

D A B 2 = D A B 1 T 2 T 1 3 / 2

D A B 2 = 0,26 × 10 - 4 × 305 298 3 / 2

D A B 2 = 0,27 × 10 - 4   m 2 / s

Passo 4

Continuando, vamos agora determinar o número de Lewis:

L e = k ρ c p D A B

L e = 0,02667 1,1448 × 100 7,2 × 0,2 7 × 10 - 4

L e = 0,857

Aplicando na analogia:

h - = h - m ρ c p L e 2 / 3

h - = 0,0113 × 1,1448 × 1007,2 × 0,857 2 / 3

h - = 11,75   W / m 2 K

A energia perdida por convecção é:

Q c o n v = h - A T s - T ∞ t

Q c o n v = 11,75 × π D 2 4 × ( 310 - 3 00 ) × ( 100 × 60 )

Q c o n v = 8,86   J

Então, a energia necessária para manter a evaporação será:

Q = Q e v + Q c o n v

Q = 90 + 8,86

Q = 98,86   J

Resposta

(a) h - m = 0,0113   m / s .

(b) Q = 98,86   J .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um dia de verão, a temperatura do ar é de 27 ° C e sua umidade relativa é de 30%. Água evapora da superfície de um lago a uma taxa de 0,10k g / m 2 ⋅ h por metro quadrado de área da sua superfície.
A taxa na qual água é perdida devido à evaporação em uma superfície de um corpo de água pode ser determinada através da medida da taxa de variação do seu nível. Considere um dia de verão no qual as te
É observado que uma panela com 230m m de diâmetro contendo água a 23 ° C apresenta uma taxa de perda de massa de 1,5 × 10 - 5k g / s , quando o ar ambiente está seco e a uma temperatura de 23 ° C .a)
A fotossíntese, como ocorre nas folhas de uma planta verde, envolve o transporte de dióxido de carbono ( C O 2 ) da atmosfera para os cloroplastos das folhas. A taxa de fotossíntese pode ser quantific
Um processo industrial envolve a evaporação de água de uma película líquida que se forma sobre uma superfície curva. Ar seco é passado sobre a película e, com base em medidas de laboratório, determino