Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 54
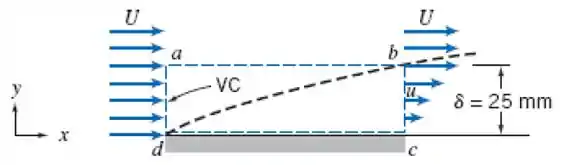
Uma camada limite de ar padrão, em desenvolvimento sobre uma placa plana, é mostrada na Fig 9.18. O escoamento de corrente livre fora da camada-limite não é perturbado com velocidade . A placa tem de largura perpendicular ao diagrama. Considere que o escoamento na camada limite é turbulento, com perfil de velocidade de potência e que na superfície . Calcule a vazão mássica através da superfície e o fluxo de massa através da superfície . Avalie o fluxo de quantidade de movimento segundo através da superfície Avalie a força de arrasto exercida sobre a placa plana entre e c. Estime a distância a partir da borda de ataque na qual a transição de laminar para turbulento pode ser esperada.
Passo 1
Vamos listar o que a gente precisa fazer:
- calcular a vazão mássica através da superfície
- calcular o fluxo de massa através da superfície . A gente pode fazer isso pela conservação de massa:
- avaliar o fluxo de quantidade de movimento segundo através da superfície
- avaliar a força de arrasto exercida sobre a placa plana entre e c:
- estimar a distância a partir da borda de ataque na qual a transição de laminar para turbulento pode ser esperada:
E enunciado dá umas informações para gente:
- escoamento turbulento
- largura:
- perfil de velocidade de lei de potência
- velocidade de corrente livre:
- expessura de perturbação em :
- ar-padrão: e
Vamos assumir também que o escoamento é permanente, que não há forças produzidas por pressão e que o fluxo é uniforme é . Vamos começar!
Passo 2
O enunciado diz que a velocidade em não é perturbado e , então a gente pode dizer que:
Ela é negativa porque tá entrando na superfície, belezinha?
Passo 3
Vamos usar a conservação de massa para achar
A gente tem o perfil de velocidade:
Passo 4
Para o fluxo da quantidade de movimento a gente usa essa expressão:
Passo 5
Podemos usar a conservação de quantidade de movimento para achar
Passo 6
Achar o de transição é achar, :