Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 50
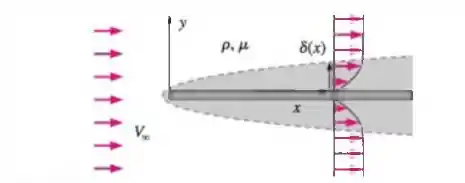
Uma camada limite é uma região fina (em geral, ao longo de uma parede longa) na qual as forças viscosas são significativas e dentro da qual o escoamento é rotacional. Considere uma
camada limite que cresce ao longo de uma placa plana fina (Figura P7-50). O escoamento é em regime permanente. A espessura da camada limite em qualquer distância a jusante é
uma função de , da velocidade de corrente livre e das propriedades do fluido (densidade) e (viscosidade). Use o método das variáveis repetidas para gerar uma relação adimensional para como função dos outros parâmetros. Mostre todo o seu trabalho.
Passo 1
Vamos lá! A gente vai usar análise dimensional para achar a relação entre a espessura da camada limite com os outros parâmetros dados!
O enunciado já deu mastigadinho pra a gente a listagem de todas as variáveis independentes que é função, então mesmo que você não seja fera em camada limite não se assuste é só a gente fazer o nosso passo a passo de sempre! Belzinha?
Então vamos começar com o primeiro passo que é listar os parâmetros relevantes!
Temos então parâmetros relevantes!!
Passo 2
Agora a gente precisa listar as dimensões primárias de cada parâmetro!
Passo 3
Quando a gente listou as dimensões primárias de cada parâmetro a gente usou as dimensões e , então podemos considerar:
Teorema de Pi de Buckingham:
O a gente já tinha achado no Passo 1, lá vimos que !
Substituindo:
Nesse caso o número de grupos esperado é igual a 2. Então vamos atrás deles!!
Passo 4
Já que vamos considerar precisamos encontrar nossos três parâmetros repetidos!
Relembrando nossos parâmetros:
De cara a gente já sabe que a gente não pode usar, pois ele é um parâmetro dependente!
Agora temos que escolher entre: e .
Vamos escolher por eles serem parâmetros mais simples!
Passo 5
Agora sim, vamos encontrar o nosso primeiro grupo !!
Começando com o que vai ser o dependente!!
Organizando os nossos parâmetros a gente fica com:
Escrevendo suas dimensões básicas:
Agora equacionando:
Massa:
Comprimento:
Tempo:
Logo:
Substituindo , e , temos:
Organizando:
Agora vamos achar , esse vai ser nosso independente combinando as nossas variáveis repetidas com :
Escrevendo suas dimensões básicas:
Agora equacionando:
Massa:
Comprimento:
Tempo:
Logo:
Substituindo temos:
Organizando:
Esse é o número de Reynolds!!!
Passo 6
Agora vamos finalmente escrever a relação entre os grupos :
Ou:
Uhuuuuuul!