Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 6

Um campo de velocidade é especificado como em que em que a = 2 m−1s−1, b = −6 m−1s−1 e as coordenadas são medidas em metros. O campo de escoamento é uni, bi ou tridimensional? Por quê? Calcule as componentes da velocidade no ponto (2,½). Deduza uma equação para a linha de corrente que passa por esse ponto. Trace algumas linhas de corrente no primeiro quadrante incluindo aquela que passa pelo ponto (2, ½).

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Este problema nos pede para obter uma equação para as linhas de corrente do escoamento e para traçarmos diversas linhas de corrente para valores no primeiro quadrante. Primeiro, vamos encontrar a dimensão do campo, Portanto:

Logo, este campo é 2D. Para a quação de linha corrente:

Agora, vamos separar as variáveis:

Integrando:

Passo 2

Com isso, nosso gráfico que passa pelo ponto . Fica assim:

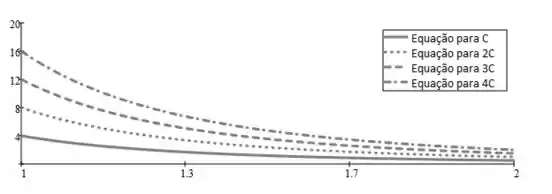
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O dispositivo na Figura P 1.56 é chamado de viscosímetro cone-placa. O ângulo do cone é muito pequeno, de forma que sen ⁡ θθ , e a folga é preenchida com o líquido de teste. O torque M necessário para

A correia na Figura P 1.52 move-se a uma velocidade constante V e desliza na parte superior de um tanque de óleo de viscosidade μ , como mostra a figura. Considerando um perfil linear de velocidade no

Foram desenvolvidos muitos equipamentos comerciais e de laboratório para medir viscosidade, como descrevem as Referências 29 e 49 . Considere um eixo concêntrico, como no Problema 1.47 , mas agora fix

Um disco de raio R gira a uma velocidade angular Ω no interior de um reservatório em forma de disco cheio com óleo de viscosidade m, como mostra a Figura P 1.54 . Considerando um perfil linear de velo

Um viscosímetro simples mede o tempo t para que uma esfera sólida caia uma distância L no interior de um fluido de teste, de massa específica r . A viscosidade μ do fluido é dada então por μ ≈ P l i q