Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas - Ex. 54
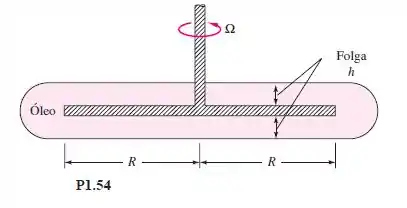
Um disco de raio R gira a uma velocidade angular no interior de um reservatório em forma de disco cheio com óleo de viscosidade m, como mostra a Figura . Considerando um perfil linear de velocidade e desprezando a tensão de cisalhamento nas bordas externas do disco, deduza uma fórmula para o torque viscoso no disco.
Passo 1
Vamos lá, podemos montar a formula para o torque viscoso.
Para qualquer , o torque viscoso é:
Para ambos os lados do disco
Onde:
Assim:
Agora temos que integrar nosso torque, vamos lá!
Finalizando nossa questão, temos:
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
Exercícios de Livros Relacionados
CConsidere o campo de escoamento dado na descrição euleriana pela expressão V → = a x î + b y t j ^ î , em que a = 0,2s - 1 , b = 0,04s - 2 e. e as coordenadas são medidas em metros. Deduza as funções
Considere a mangueira de jardim da Figura 2.5. Suponha que o campo de velocidade é dado por V → = u 0 î +v 0 s e n [ ω ( t-x / u 0) ] j ^ î , onde a direção x é horizontal e a origem está na posição m
As linhas de emissão são visualizadas por meio de um fluido corante de empuxo neutro injetado em um campo de escoamento a partir de um ponto fixo no espaço. Uma partícula do fluido corante que está no
Um escoamento é descrito pelo campo de velocidade V =a x i+b j , em que a=1 / 5s- 1 b=1m / s . As coordenadas são medidas em metros. Obtenha uma equação para a linha de corrente que passa através do p
Um escoamento é descrito pelo campo de velocidade V =a y i+b t j , em que a=0,2s - 1 e b=0,4 m / s 2 . Em t=2s , quais são as coordenadas da partícula que passou pelo ponto (1, 2) em t = 0. Em t=3s ,