Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas - Ex. 49

Foram desenvolvidos muitos equipamentos comerciais e de laboratório para medir viscosidade, como descrevem as Referências 29 e 49 . Considere um eixo concêntrico, como no Problema 1.47 , mas agora fixado axialmente e girando no interior do mancal. Sejam os raios interno e externo dos cilindros r i e r o , respectivamente, tendo o mancal um comprimento total L . Seja a velocidade angular Ω   ( r a d / s ) e seja M o torque aplicado. Usando esses parâmetros, deduza uma relação teórica para a viscosidade μ do fluido na folga entre os cilindros.

Passo 1

Primeiro vamos fazer um esquema da nossa questão para ilustrar nosso problema:

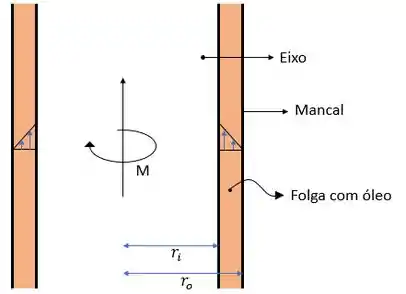
Nossa questão nos pede a dedução da viscosidade μ em função dos parâmetros dados, bora resolver isso!

Passo 2

Vamos assumir que a distribuição de velocidade é linear para o fluído, para facilitar nosso trabalho!

Assim temos:

τ = μ ⋅ Δ V Δ r ≈ μ ⋅ Ω r i r o - r i

Essa tensão resulta em uma força d F = τ d A = τ r i d θ L em cada elemento de área na superfície do eixo então vamos integrar.

Mas temos que lembrar que d M = r i d F

Passo 3

Vamos integrar nossa equação, assim temos:

M = ∫ r i ⋅ d F = ∫ 0 2 π r i ⋅ μ ⋅ Ω r i r o - r i ⋅ r i ⋅ L ⋅ d θ

Integrando:

M = 2 ⋅ π ⋅ μ ⋅ Ω ⋅ r i 3 ⋅ L r o - r i

Vamos isolar o coeficiente de viscosidade μ , para matarmos essa questão de vez!

μ =   M r o - r i 2 π μ Ω r i 3 L

Isso é tudo pessoal, essa foi rápida! \o/

Resposta

μ =   M r o - r i 2 π μ Ω r i 3 L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o campo de escoamento dado na descrição euleriana pela expressão V = A î - B t j ^ î , em que A=2m / s , B = 2m / s 2 e as coordenadas são medidas em metros. Deduza as funções de posição lag
0 Considere o campo de escoamento V =a x t i+b j , em que a= 1 4 s - 2 e b=1 / 3m / s . As coordenadas são medidas em metros. Para a partícula que passa pelo ponto ( x ,y )=( 1 ,2 ) no instante t=0 ,
Considere o campo de velocidade do Problema 2.20. Trace a linha de emissão formada por partículas que passaram pelo ponto ( 1 ,1 ) durante o intervalo de tempo de t=0 a t=3s . Compare com as linhas de
Um escoamento é descrito pelo campo de velocidade = at + b , em que a=0,4m / 2 e b=2m / s . Em t=2s , quais são as coordenadas da partícula que passou pelo ponto (2, 1) em t = 0? Em t=3s , quais são a
Considere o campo de velocidades V → = a x î + b y ( 1+c t ) j ^ î , em que a = b = 2s - 1 e c = 0,4s - 1 . As coordenadas são medidas em metros. Para a partícula que passa pelo ponto ( x ,y ) =( 1 ,1