Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas - Ex. 52
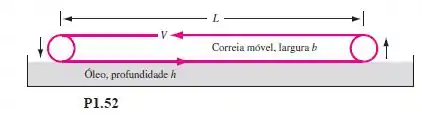
A correia na Figura move-se a uma velocidade constante e desliza na parte superior de um tanque de óleo de viscosidade , como mostra a figura. Considerando um perfil linear de velocidade no óleo, desenvolva uma fórmula simples para a potência necessária para o acionamento da correia em função de . Qual é a potência necessária para o acionamento da correia se ela se move a em óleo a , com , e?
Passo 1
Vamos lá, podemos montar a formula da potência da força de atrito viscoso da seguinte forma.
Passo 2
Agora substituir na nossa equação com os valores dados apresentados na questão.
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
Exercícios de Livros Relacionados
Considere o escoamento descrito pelo campo de velocidade V → = B x ( 1+A t ) î +C y j ^ î , com A=0,5s - 1 e B = C=1s - 1 . As coordenadas são medidas em metros. Trace a trajetória da partícula que pa
Um campo de velocidade é dado por V → =a y t î - b x j ^ î , em que a = 1s - 2 eb = 4s - 1 . Determine a equação das linhas de corrente para qualquer tempo t . Trace algumas curvas para t = 0s ,t = 1s
O campo de escoamento para um escoamento atmosférico é dado por V → = - K y 2 π ( x 2 + y 2 ) î + K x 2 π ( x 2 + y 2 ) j ^ î em que K=10 5m 2 / s e as coordenadas x e y são paralelas à latitude e lon
Um campo de escoamento é dado por V → = - q x 2 π x 2 + y 2 î - q y 2 π ( x 2 + y 2 ) j ^ î em que q=5×10 4m 2/ s . Trace um gráfico com o módulo da velocidade ao longo do eixo x, ao longo do eixo y e
Usando os dados do Problema 2.26, determine e trace a forma da linha de emissão produzida após o primeiro segundo de escoamento.