Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas - Ex. 80
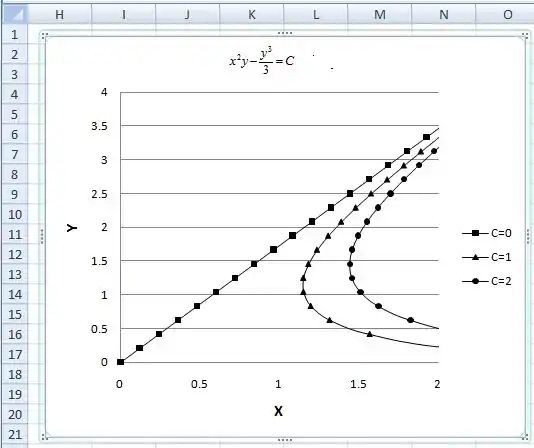
Um campo de velocidade permanente bidimensional é dado por . Deduza o campo de linhas de corrente e esboce algumas linhas de corrente no semiplano superior.
Dica: a equação diferencial é exata.
Passo 1
Bem, vamos lembrar que a equação apresentada é uma equação diferencial de segunda ordem, então podemos organizar ela para ela tomar essa cara!
Rearranjando os termos, temos:
Passo 2
Agora antes de integrar essa equação diferencial temos que verificar o critério das derivadas, assim:
Como visto nossa equação diferencial é exata, logo podemos integrar qualquer uma das equações dadas:
Para esboço do gráfico recomendo o uso do webapp do geogebra, para plot de gráficos em 3d
Isso é tudo pessoal, conseguimos mais uma! \o/
Passo 3
Resposta
Exercícios de Livros Relacionados
An airplane fl ies at 555 mi/h. At what altitude in the standard atmosphere will the airplane’s Mach number beexactly 0.8?
Extend the steady fl ow between a fi xed lower plate and amoving upper plate, from Fig. 1.7, to the case of twoimmiscible liquids between the plates, as in Fig. P1.57.h2yx h1 µ1µ2VFixedP1.57(a) Sketch
Pressure in a water container can be measured by an open vertical tube—see Fig. P2.11 for a sketch. If the expected waterrise is about 20 cm, what tube diameter is needed to ensure thatthe error due t
Use Eq. (1.39) to fi nd and sketch the streamlines of thefollowing flow fi eld:u 5 K(x2 2 y2); v 5 22Kxy; w 5 0, where K is a constant.Hint: This is a first-order exact differential equation.
In Problem P1.24, for the given data, the air velocity at section 2 is 1180 ft/s. What is the Mach number at that section?