Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 19

Para o campo de velocidade do Problema 4-2, calcule a aceleração do fluido ao longo do eixo central do bocal como função de x e dos parâmetros dados.

Passo 1

A questão pede para a gente calcular a aceleração do fluido ao longo do eixo central x a x de um escoamento do Problema 4-2. Nesse problema, calculamos o valor da velocidade u x do fluido ao longo do eixo central de um bocal em função da velocidade u e n t r a d a do fluido a x = 0 e da velocidade u s a í d a do fluido a x = L . A imagem abaixo mostra o bocal.

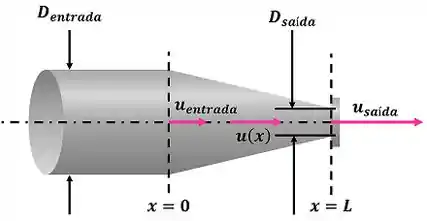
D e n t r a d a é o diâmetro de entrada do bocal e D s a í d a é o diâmetro de saída do bocal.

A velocidade u x do fluido no eixo central é calculada no problema 4-2. Ela vale:

u x = u e n t r a d a + u s a í d a - u e n t r a d a L 2 ⋅ x 2

No próximo passo nós vamos aprender a calcular a aceleração a partir dessa velocudade u x .

Passo 2

O enunciado quer que a gente calcule a x do eixo central a partir da velocidade u x do eixo central encontrada no Problema 4-2. Como a aceleração do fluido a → é igual à derivada material da velocidade D V → D t , podemos calcular a → derivando a equação de V → dada pela questão 4-2.

A equação 4 - 11 do livro calcula esse valor.

a x = ∂ u ∂ t + u ⋅ ∂ u ∂ x + v ⋅ ∂ u ∂ y + w ⋅ ∂ u ∂ z

onde u é a componente do eixo x da velocidade V → , v é a componente do eixo y da velocidade V → e w é a componente do eixo z da velocidade V → . Como o escoamento na linha de centro só depende da variável x :

∂ u ∂ y = 0

∂ u ∂ z = 0

Além disso, o enunciado da questão 4-2 diz que o escoamento é estacionário. Isso significa que a velocidade do escoamento não varia com o tempo.

∂ u ∂ t = 0

Substituindo essas informações na equação de a x , encontramos:

a x = u ⋅ ∂ u ∂ x

Passo 3

A equação de a x depende de ∂ u ∂ x . ∂ u ∂ x pode ser calculado a partir da equação de u x .

∂ u ∂ x = ∂ ∂ x u e n t r a d a + u s a í d a - u e n t r a d a L 2 ⋅ x 2       ⟹       ∂ u ∂ x = 2 ⋅ u s a í d a - u e n t r a d a L 2 ⋅ x

Agora podemos substituir a equação da velocidade u x e de ∂ u ∂ x na equação de a x para encontrar uma fórmula para a x .

a x = u ⋅ ∂ u ∂ x       ⟹       a x = u e n t r a d a + u s a í d a - u e n t r a d a L 2 ⋅ x 2 ⋅ 2 ⋅ u s a í d a - u e n t r a d a L 2 ⋅ x

a x = 2 ⋅ u e n t r a d a ⋅ u s a í d a - u e n t r a d a L 2 ⋅ x + 2 ⋅ u s a í d a - u e n t r a d a 2 L 4 ⋅ x 3

Resposta

a x = 2 ⋅ u e n t r a d a ⋅ u s a í d a - u e n t r a d a L 2 ⋅ x + 2 ⋅ u s a í d a - u e n t r a d a 2 L 4 ⋅ x 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use dois métodos para verificar se o escoamento do Problema 4-55 é incompressível: ( a ) calculando o volume da partícula de fluido em ambos os instantes e ( b ) calculando a taxa de deformação volumé
Considere o campo de velocidade estacionário, incompressível e bidimensional do Problema 4-55. Usando os resultados do Problema 4-55 ( a ) faça o seguinte: ( a ) Da definição fundamental de taxa de ro
O escoamento de duto convergente é modelado pelo campo de velocidade em regime permanente e bidimensional do Problema 4-15. À medida que o seguimento de reta vertical A B se movimenta a jusante, ele e
Considere o campo de velocidade estacionário, incompressível e bidimensional do Problema 4-55. Usando os resultados do Problema 4-55 ( a ) faça o seguinte: ( a ) Da definição fundamental de taxa de de
Um elemento de fluido bidimensional de dimensões d x e d y é translado e distorcido como mostra a Figura P4-60 durante o período de tempo infinitesimal d t = t 2 - t 1 . As componentes da velocidade n