Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 56
Use dois métodos para verificar se o escoamento do Problema 4-55 é incompressível: calculando o volume da partícula de fluido em ambos os instantes e calculando a taxa de deformação volumétrica. Observe que o Problema 4-55 deve ser feito antes deste problema.
Passo 1
Para resolvermos a questão iremos precisar da equação abaixo, onde o volume da partícula de fluido no momento pode ser expresso como sendo:
Onde é o comprimento da partícula de fluido na direção z.
Passo 2
No momento , assumimos que a dimensão da partícula do fluido permanece fixa, pois o fluxo é bidimensional. Assim, seu volume é vezes a área do losango mostrada na figura abaixo.
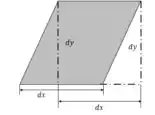
Desde que as equações 1 e 2 sejam iguais, o volume da partícula de fluido não mudara e, portanto, o fluxo é incompressível.
Passo 3
Para a questão usaremos a equação para taxa de deformação volumétrica em coordenadas cartesianas e aplicaremos os resultados do problema anterior...
Onde , pois o fluxo é bidimensional. Como a taxa de deformação volumétrica é zero em todos os lugares, o fluxo é incompressível.
Resposta
Ei, a resposta está no passo a passo :)