Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 50
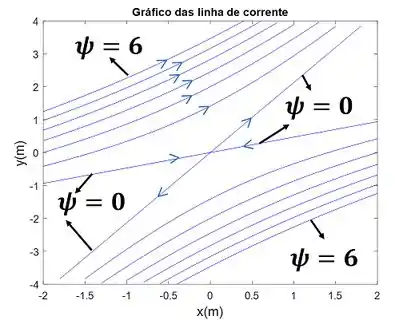
Para o campo de velocidade do Problema 9-49, faça o gráfico das linhas de corrente e . Considere as constantes , e com os seguintes valores: , e . Por consistência, desenhe as linhas de corrente entre e , e e . Indique a direção do escoamento com setas.
Passo 1
O exercício quer que a gente desenhe em um gráfico uma linha de corrente para cada valor de função corrente : e . Para fazer isso, temos que usar a expressão de função corrente presente no Problema 9-49 que está abaixo.
Desenhar as linhas de corrente em um gráfico é o mesmo que calcular a posição de cada ponto que forma a linha de corrente (ou seja, calcular as coordenadas de cada ponto que forma uma linha de corrente com valor de constante). Em outras palavras, precisamos encontrar o valor da coordenada da linha de corrente para cada valor de e .
Encontrar os valores de para certos valores de é a mesma coisa que encontrar os zeros da equação abaixo. Essa equação é apenas a equação anterior com do outro lado da equação.
Substituímos os valores de , e na equação, ela vira:
No passo seguinte vamos entender o processo de cálculo das raízes para formar o gráfico das linhas de corrente.
Passo 2
Para encontrar os valores dos zeros da equação acima precisamos usar a fórmula de Bhaskara de polinômios do segundo grau. Como calculamos os valores para cada valor de e , e fazem parte das constantes do polinômio para o qual temos que achar as raízes.
onde , e são os símbolos dos coeficientes do polinômio de segundo grau e não devem ser confundidos com os coeficientes , e da expressão da função corrente .
A fórmula de Bhaskara se encontra abaixo.
Os valores de devem variar de e e geraremos o gráficos para valores de entre e .
Passo 3
Além de desenhar as linhas de corrente, o problema também pede que a gente indique a direção do escoamento com setas. Para fazer isso, temos que calcular as componentes (componente do eixo ) e (componente do eixo ) da velocidade do escoamento. Fazemos isso, derivando a função corrente de acordo com a equação 9-20 do livro para escoamentos incompressíveis e bidimensionais.
Substituindo as expressões de nessas fórmulas, encontramos expressões para e .
Com essas equações, descobrimos para onde a velocidade de cada ponto do escoamento aponta. Vamos considerar o ponto onde e como exemplo. Nesse ponto, os valores de e valem:
Como é positivo, o sentido do escoamento no eixo no ponto é da esquerda pra direita. Se fosse negativo, o sentido do escoamento no eixo no ponto seria da direita para a esquerda. Como é positivo, o sentido do escoamento no eixo no ponto é de baixo pra cima. Se fosse negativo, o sentido do escoamento no eixo no ponto seria de cima pra baixo.
Passo 4
O gráfico resultante é mostrado abaixo.
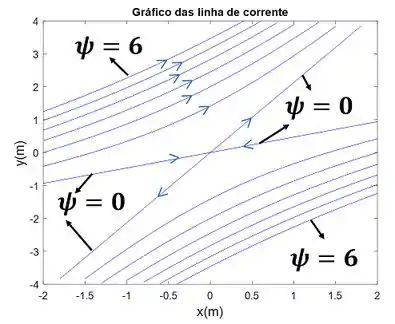
Resposta
