Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 45

Suponha que a sucção aplicada à sonda de amostragem do Problema 9-44 fosse muito fraca em vez de muito forte. Faça um desenho de como deveríam ser as linhas de corrente nesse caso. Como você chamaria esse tipo de amostragem? Identifique as linhas de corrente divisórias superior e inferior.

Passo 1

O exercício quer saber como seria o desenho das linhas de corrente que atravessam a sonda caso a sucção fosse fraca ao invés de forte.

Para entender isso, precisamos entender o que é uma sucção fraca e e o que é uma sucção forte.

Uma sucção forte quer dizer que a velocidade do fluido aumentou ao entrar na sonda.

Uma forma de visualizar esse aumento de velocidade do fluido é observando as linhas de corrente do escoamento. Se as linhas de corrente diminuem de espaçamento ao entrar na sonda, a velocidade do fluido aumentou. Podemos fazer essa afirmação, porque o fluido está forçando uma mesma vazão através de uma área menor (a área diminui, por causa da aproximação das linhas de corrente). A figura abaixo ilustra esse processo.

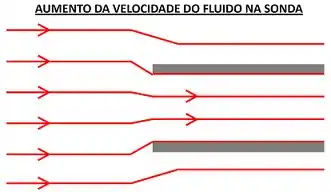
Como podemos ver, é como se as linhas de corrente tivessem que ser espremidas para caber em uma área de escoamento menor. Isso faz com que a velocidade média do fluido aumente. É só lembrar do que acontece, quando tampamos parcialmente uma mangueira com o dedo. A velocidade da água aumenta, porque a área de passagem dela passa a ser menor!

Esse tipo de processo de aumento da velocidade com a sucção é chamada de amostragem superisocinética. O prefixo “super” usado para nomear esse tipo de amostragem é necessário para lembrar que a velocidade aumenta em relação à velocidade do escoamento fora da sonda.

Passo 2

Uma sucção fraca quer dizer que a velocidade do fluido diminuiu ao entrar na sonda.

Se as linhas de corrente se aproximam, quando a velocidade do fluido aumenta, o que aconteceria com elas caso a velocidade do fluido diminuísse? Ou seja, se acontecesse o inverso do caso anterior de aumento da velocidade, o que aconteceria com as linahs de corrente?

Quando acontece o inverso do aumento de velocidade (diminuição da velocidade), as linhas de corrente se comportam de maneira inversa ao comportamento observado ao crescimento da velocidade (diminuição do espaçamento entre as linhas de corrente). Em outras palavras, quando a velocidade do fluido diminui ao entrar na sonda, as linhas de corrente ficam mais espaçada. Isso é mostrado na figura abaixo.

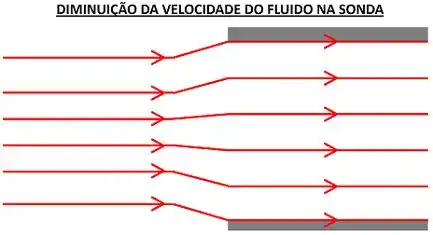
Para mostrar que a velocidade diminui a entrar na sonda, usamos substituímos o prefixo “super” pelo prefixo “sub”. Ou seja, essa amostragem é chamada de amostragem subisocinética.

Resposta

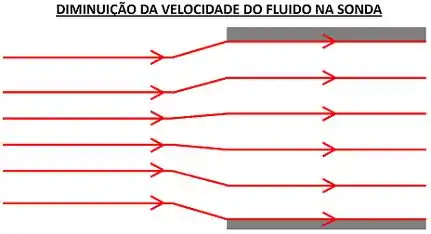
Essa amostragem é chamada de subisocinética.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um campo de escoamento é representado pela função de corrente ψ = x 5 - 10 x 3 y 2 + 5 x y 4 . Determine o campo de velocidade correspondente. Mostre que este campo de escoamento é irrotacional e obte

A função de corrente de um campo de escoamento é ψ = A x 2 y - B y 2 , em que A = 1 m - 1 . s - 1 , B = 1 3m - 1 . s - 1 e as coordenadas são medidas em metros. Encontre uma expressão para o potencial

A função de corrente de um campo de velocidade é ψ = A x 3 + B ( x y 2 + x 2 - y 2 ) , em que ψ , x , y , A e B são todos adimensionais. Encontre a relação entre A e B para esse escoamento. Encontre o

A função de corrente de um campo de velocidade é ψ = A x 3 - B x y 2 , em que A = 1m - 1 . s - 1 e B = 3m - 1 . s - 1 , e as coordenadas são medidas em metros. Encontre a expressão para o potencial de

Considere o campo de escoamento representado pela função potencial φ = A x 2 + B x y - A y 2 . Verifique se esse é um escoamento incompressível, e determine a função de corrente correspondente.