Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 110

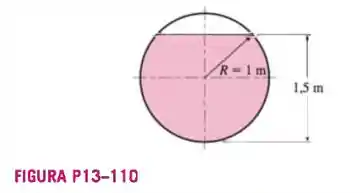
Um canal de drenagem de aço circular com 2 m de diâmetro interno (n = 0,012) deve descarregar água de modo uniforme a uma vazão de 12 m³/s até uma distância de 1 km. Se

a profundidade máxima deve ser 1,5 m, determine a queda de elevação necessária.

Passo 1

Opaa, vamos lá!!

Queremos descobrir a queda de elevação em uma tubulação de 1   k m de um canal circular! Para isso fazemos:

Δ z = S o L

Onde S o é o parâmetro referente a inclinação e L é o comprimento da tubulação, vamos dar uma olhadinha na secção transeversal desse tubo:

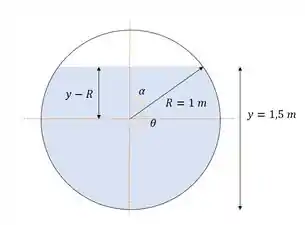
O S o aparece na equação de Manning:

V ˙ = a n × A c R h 2 3 S o 1 2

Podemos isolar ele:

S o = V ˙ n a 1 A c 1 R h 2 3 2    

Passo 2

Agora precisamos achar a área transversal, A c e o raio hidráulico R h !

A área transversal é dada por:

A c = R 2 θ - sin ⁡ θ cos ⁡ θ

Mas não conhecemos θ :

θ = π - α

Podemos calcular α :

cos ⁡ α = y - R R = 1,5 - 1 1 = 0,5

Calculando o cos - 1 ⁡ 0,5 achamos α = 60 ° , que pode ser escrito como α = π / 3 , logo:

θ = π - π 3 = 2 π 3

E finalmente:

A c = 1 2 2 π 3 - sin ⁡ 2 π 3 cos ⁡ 2 π 3 = 2,527   m 2

Agora, para calcular o raio hidráulico:

R h = A c p = A c 2 θ R

Substituindo:

R h = 2,527 2 × 2 π 3 × 1 = 0,60 3   m

Passo 3

Agora podemos calcular S o , relembrando:

S o = V ˙ n a 1 A c 1 R h 2 3 2    

Se, a = 1   m 1 3 / s   e n = 0,012 , então:

S o = 12 × 0,012 1 × 1 2,527 × 1 0,6034 2 3 2    

E finalmente achamos Δ z :

Δ z = 0,0067 × 1000 = 6,37   m

Aweee!!!

Resposta

Δ z = 6,37   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13-116 Água escoa de modo uniforme a meia carga em um canal circular com 1,2 m de diâmetro assentado com uma inclinação de 0,004. Se a vazão da água for medida como 1,25 m³/s, determine o coeficiente
Reconsidere o Problema 13-117. Determine a altura da saliência para a qual o escoamento sobre ela é crítico (Fr = 1).
13-121 Água escoando em um canal largo a uma profundidade de escoamento de 45 cm e uma velocidade média de 8 m/s sofre um salto hidráulico. Determine a fração de energia mecânica do fluido dissipada d
Água escoando através de uma comporta basculante passa por um salto hidráulico, como mostra a Figura P13-124. A velocidade da água é 1,25 m/s antes de atingir a comporta e 4 m/s após o salto. Determin
13-117 Água escoando em um canal horizontal largo se aproxima de uma saliência com 20 cm de altura a uma velocidade de 1,25 m/s e profundidade de escoamento de 1,8 m. Determine avelocidade, a profundi