Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 118
Reconsidere o Problema 13-117. Determine a altura da saliência para a qual o escoamento sobre ela é crítico (Fr = 1).
Passo 1
Bora relembrar o problema anterior!! Tinhamos o seguinte escoamento:
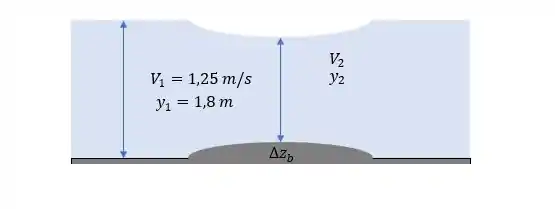
Agora a gente quer achar para que o escoamento sobre a saliência seja crítico, ou seja !
Temos então:
Como o escoamento é crítico em cima da saliência então podemos dizer que:
Passo 2
No problema anterior achamos:
Agora podemos calcular :
Mas para isso precisamos conhecer :
Substituindo:
Agora calculamos :
Passo 3
Finalmente podemos calcular a altura da saliência:
Aweee!!!
Resposta
Exercícios de Livros Relacionados
Um canal retangular feito de tijolos com S 0 = 0,002 é projetado para conduzir 6,51m 3 / s de água em escoamento uniforme. Discute-se se a largura do canal deverá ser de 1,22 ou 2,44 m. Qual projeto q
Usando a geometria da Figura 10.6a, prove que o canal circular abeto mais eficiente (raio hidráulico máximo para uma dada área de escoamento) é um semicírculo.
Em períodos de cheia, um canal natural frequentemente consiste em uma calha principal profunda mais duas calhas de cheia, como mostra a Figura P10.35. As calhas de cheia em geral são rasas e rugosas.
O cálculo nos diz que a profundidade de água mais eficiente para um canal retangular (como na Figura E10.1) é y b = 1 2 . Ela produz a vazão normal mais alta para uma dada área. Mas esse ponto de máxi
Um canal com a forma de meio V tem o mesmo desempenho de um canal em V completo? A resposta do Problema P10.24 é y n = 0,56m . (Não revele isso aos seus colegas que ainda estão trabalhando no P10.24.)