Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 4.Problemas - Ex. 54
Um canal por onde passam gases quentes de exaustão possui uma seção transversal quadrada de 300 mm de lado. As paredes são construídas com tijolos refratários com 150 mm de espessura e uma condutividade térmica de 0,85 W/(m-K). Calcule a perda de calor dos gases, por unidade de comprimento, quando as superfícies interior e exterior do canal são mantidas a 350e 25°C, respectivamente. Use uma malha com espaçamento de 75 mm.
Passo 1
Iai gente! Prontos pra detonar mais uma questão comigo? Bora lá!
Podemos usar a simetria do sistema como vantagem para calcular mais facilmente essa questão. Assim, pra obter a taxa de calor, primeiro precisamos determinar as temperaturas 1, 2, 3 e 4. Reconhecendo que esses nós podem ser tratados como nós internos, as equações nodais retiradas da Eq. 4.29 do livro são:
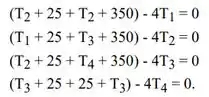
Podemos usar o método das iterações de Gauss-Seidel para resolver esse tipo de equações, seguindo o processo que foi melhor explicadinho na Seção 4.5.2 do livro. Podemos reescrever essas equações como sendo:
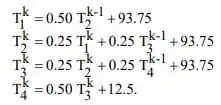
Passo 2
As estimativas iniciais (k = 0) são cuidadosamente escolhidas para minimizar o trabalho de cálculo; seja .
Pra gente conhecer a distribuição de temperaturas, podemos somar as taxas de calor através do controle de volume das superfícies nodais, como mostrado nesse esqueminha abaixo:
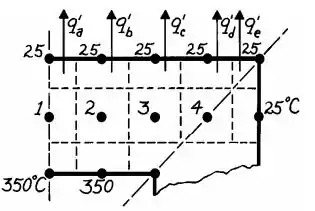
Passo 3
A taxa de calor deixando a superfície externa da seção de combustão pode ser determinada como:
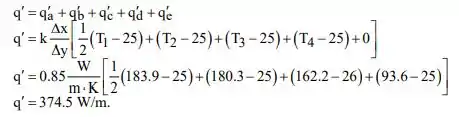
Uma vez que a seção de combustão é 1/8 da seção total, a perda de calor total da combustão é a seguinte:
Ou seja:
Espero que tenham curtido! Nos vemos na próxima questão, galera!