Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 5.Problemas - Ex. 109
Seja a placa espessa de cobre no Exemplo 5.10, que se encontra inicialmente a uma temperatura uniforme de 20°Ce é subitamente exposta a uma grande vizinhança a 1000°C (em vez de um fluxo térmico especificado).
(a) Para uma emissividade na superfície de 0,94, calcule as temperaturas r (0, 120 s) e 7X0,15 m; 120 s) usando uma abordagem de elementos finitos. Lembre-se que todas as temperaturas devem estar em kelvins.
(b) Represente os históricos de temperatura em x = 0, 150 e 600 mm, e explique características importantes dos seus resultados.
Passo 1
Iai gente! Prontos pra detonar mais uma questão comigo? Bora lá!
a) Usando o software para calcular FEHT, um contorno da laje é desenhado com espessura de 600 mm na direção x e comprimento arbitrário na direção y. Basta então clicarmos em Configuração | Temperaturas em K, para inserir todas as temperaturas em kelvins. As condições de contorno são especificadas da seguinte forma: nos planos y e no plano x = 600 mm, tratando como adiabático; na superfície (0,y), selecione a opção de coeficiente de convecção, para então inserir o coeficiente linearizado de radiação definido pela Eq. 1.9 como:
O próximo passo é entrar com as temperaturas de vizinhança, 1273 K, na caixa de temperatura de fluido. Indo nas opções VIEW | TEMPERATURES, encontramos os seguintes resultados:
Passo 2
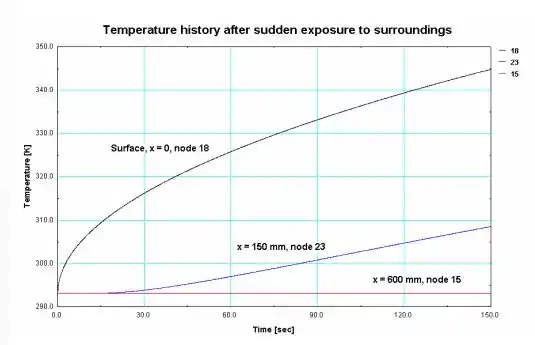
b) Usando as opções VIEW | TEMPERATURES, os históricos de temperatura para x = 0, 150 e 600 mm (10 mm de malha, nós 18, 23 e 15, respectivamente) são plotados. Como esperado, a temperatura da superfície aumenta acentuadamente nos primeiros tempos. Como a penetração térmica aumenta com o aumento do tempo, a temperatura no local x = 150 mm começa a aumentar após cerca de 30 s. Podemos notar, no entanto, que a temperatura no local x = 600 mm não muda significativamente dentro dos 150 s de exposição ao
ambientes quentes. Nossa suposição de tratar o limite no plano x = 600 mm como adiabático é
justificada! Uma placa de cobre de 600 mm é uma boa aproximação para um meio semi-infinito, às vezes menor que 150 seg.
Passo 3
Um print da tela do software pode ser visualizado abaixo:
Espero que tenham curtido! Nos vemos na próxima questão, galera!