Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 105
Características específicas de materiais biologicamente ativos, como frutas, vegetais e outros produtos, fazem com que eles necessitem de cuidado especial no manuseio. Após a colheita e a separação das plantas produtoras, a glicose é catabolizada, produzindo dióxido de carbono, vapor d’água e calor, com a consequente geração interna de energia. Seja uma caixa de maçãs, cada uma com 80 mm de diâmetro, que é ventilada com ar a 5°C e a uma velocidade de 0,5 m/s. O valor correspondente do coeficiente de transferência de calor é de 7,5 W/(m² · K). No interior de cada maçã, energia térmica é gerada uniformemente a uma taxa total de 4000 J/(kg · dia). A massa específica e a condutividade térmica da maçã são 840 kg/m³ e 0,5 W/(m · K), respectivamente.
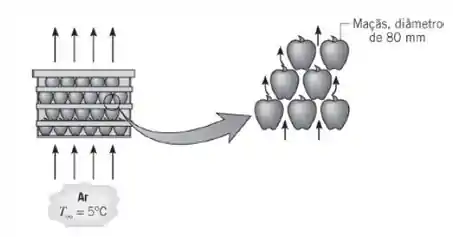
(a) Determine as temperaturas no centro e na superfície das maçãs.
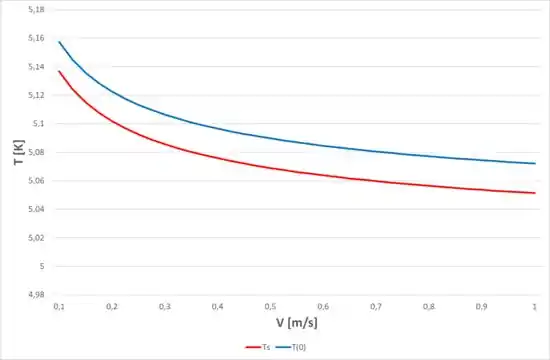
(b) Para uma pilha de maçãs no interior de uma caixa, o coeficiente convectivo depende da velocidade do ar na forma , na qual . Calcule e represente graficamente as temperaturas no centro e na superfície das maçãs em função da velocidade do ar para 0,1 ≤ V ≤ 1 m/s.
Passo 1
Tá legal! Para começar a letra (a) vamos escrever a equação para o perfil de temperatura nas maçãs. Vamos modelar cada uma delas como se fosse uma esfera, então, nesse caso, onde temos uma esfera e geração, o perfil de temperatura pode ser escrito como:
Então, aplicando um balanço de energia na maça, nós temos que o calor gerado no sistema será trocado por convecção, então, podemos escrever:
Então, abrindo as expressões, chegamos em:
Passo 2
Agora, precisamos encontrar a taxa de geração volumétrica para cada maçã em , então, convertendo o dado que foi dado, temos:
Agora, vamos substituir os valores conhecidos na equação obtida no passo 1, dessa forma, temos:
Agora então podemos encontrar a temperatura no centro das maçãs, utilizando o perfil de temperatura descrito no passo 1, então, em , teremos:
Passo 3
Agora, para a letra (b), nós iremos aplicar o mesmo balanço de energia aplicado no passo 1, chegando em:
Só que agora, nós temos o coeficiente convectivo como sendo:
Então, a equação acima se torna:
E, vamos substituir essa expressão na equação para o perfil de temperatura, então, teremos:
E, fazendo para obter a temperatura no centro das maçãs, a equação acima se torna:
Agora, vamos plotar as duas temperaturas, tanto na superfície, quanto no centro das maçãs, com o auxílio das equações acima, para o intervalo de velocidade de interesse. Dessa forma, teremos:
