Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 107
O medidor de calor radiante mostrado na figura é feito com uma folha metálica de constantan, pintada de preto e com o formato de um disco circular com raio R e espessura t. O medidor é posicionado em um envoltório onde há vácuo. O fluxo de radiação incidente absorvido pela folha, , difunde-se em direção à circunferência externa e ao grande anel de cobre, que atua como um sumidouro de calor a uma temperatura constante T(R). Dois fios de cobre estão fixados ao centro da folha e ao anel, fechando um circuito de termopar que permite a mediação da diferença de temperaturas entre o centro da folha e a sua extremidade, ΔT = T(0) – T(R).
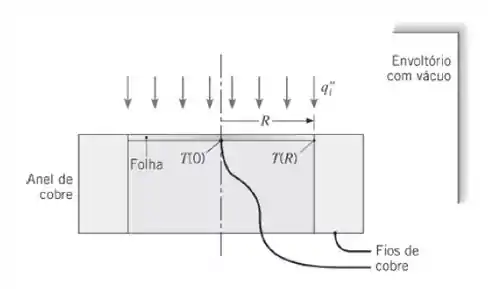
Obtenha a equação diferencial que determina T(r), a distribuição de temperaturas na folha, em condições de regime estacionário. Resolva essa equação para obter uma expressão que relacione ΔT com . Você pode desprezar a troca de calor por radiação entre a folha e a sua vizinhança.
Passo 1
Tá legal! Vamos começar esse exercício aplicando o princípio da conservação de energia para um anel circular que vai de até , dessa forma, o calor que entra em mais a parcela que entra por será igual ao calor que sai em , então, podemos escrever:
No entanto, podemos escrever o calor em pelo princípio de Fourier, já que temos condução, então, teremos:
Podemos escrever agora a parcela de calor em como sendo o calor em mais a variação nesse trecho, então, teremos:
Então, substituindo as expressões encontradas na equação para o equilíbrio de energia, temos:
Simplificando essa expressão, conseguimos chegar em:
Passo 2
Agora nós vamos integrar a expressão obtida no passo 1 em , dessa forma, temos:
Integrando novamente em , chegamos em:
Agora precisamos encontrar o valor das constantes e . Para isso, vamos utilizar duas condições de contorno. A primeira delas é que não há gradiente de temperatura em , então, temos:
Substituindo esses valores na expressão encontrada, temos:
A outra condição de contorno será a de que, em , nós temos , então, substituindo esses valores na expressão para o perfil de temperatura, temos:
Então, o perfil de temperatura será:
Passo 3
Agora vamos calcular a temperatura em na equação encontrada no passo 2, para escrever em função dos parâmetros dados no enunciado, então, teremos:
Sabendo que temos:
A equação acima se torna: