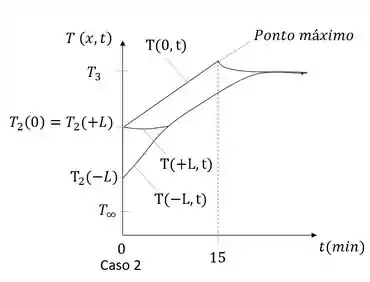
Um aquecedor elétrico delgado, dissipando , encontra-se imprensado entre duas placas, ambas com espessura de , cujas superfícies expostas trocam calor por convecção com um fluido a e As propriedades termofísicas do material das placas são e

(a) Em coordenadas , esboce a distribuição de temperaturas no regime estacionário para . Calcule os valores das temperaturas nas superfícies, , e no plano central, . Identifique essa distribuição como Caso 1 e explique suas características marcantes.

(b) Considere condições nas quais haja uma perda de refrigerante e a existência de uma condição aproximadamente adiabática na superfície . Nas coordenadas usadas na parte (a), esboce a distribuição de temperaturas no regime estacionário correspondente e indique as temperaturas em e . Identifique essa distribuição como Caso 2 e explique suas características importantes.

(c) Com o sistema operando como descrito na parte (b), a superfície também passa por uma perda súbita de resfriamento. Essa situação perigosa ficou sem ser percebida por minutos, quando então a potência do aquecedor foi desativada. Considerando a inexistência de perda de calor pelas superfícies das placas, qual será a distribuição de temperaturas nas placas, uniforme e em estado estacionário, após um longo período de tempo ? No seu esboço, mostre essa distribuição como Caso 3 e explique suas características marcantes. Sugestão: Aplique a exigência de conservação de energia com base em um intervalo de tempo, Equação 1.12b, com as condições inicial e final correspondendo aos Casos 2 e 3, respectivamente.

(d) Em coordenadas , esboce o histórico da temperatura, nas posições das placas e , ao longo do período transiente entre as distribuições dos Casos 2 e 3. Onde e quando a temperatura no sistema atinge um valor máximo?

Antes de tudo, nós vamos assumir que a condução é unidimensional, as propriedades são constantes, não ocorre geração volumétrica interna em placas e a resistência térmica é desprezível entre as superfícies do aquecedor e as placas.

Na letra (a) queremos a distribuição de temperaturas no regime estacionário para e os valores das temperaturas nas superfícies, , e no plano central, . Como o sistema é simétrico, a potência do aquecedor resulta em fluxos de condução iguais através das placas. Aplicando um balanço de energia na superfície , vamos determinar as temperaturas no ponto médio, , e na superfície exposta, .

Onde,

Então:

Da Lei de Fourier para o fluxo de condução através da placa, encontramos :

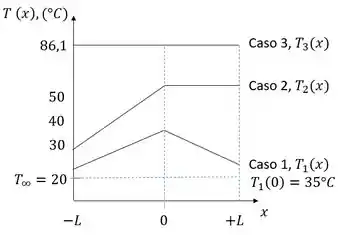
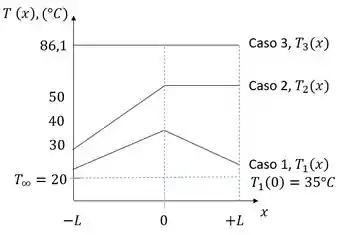
A distribuição de temperatura é mostrada nas coordenadas abaixo e identificada como Caso 1. Os principais recursos da distribuição são sua simetria sobre o plano do aquecedor e sua dependência linear com a distância.

Na letra (b) queremos a distribuição de temperaturas no regime estacionário correspondente e indicar as temperaturas em e . Então nesse caso 2 temos perda repentina de líquido de refrigeração com a existência de uma condição adiabática na superfície x = + L. Para esta situação, toda a energia do aquecedor será conduzida para o líquido de arrefecimento pela placa esquerda. No balanço de energia superficial e na aplicação da lei de Fourier, conforme feito na parte (a), encontramos:

A distribuição de temperatura é mostrada nas coordenadas do passo anterior e identificada como Caso 2. A distribuição é linear na placa esquerda, com o valor máximo no ponto médio. Como nenhum calor flui através da placa direita, o gradiente deve zero e esta placa também está na temperatura máxima. A temperatura máxima é mais alta que no caso 1, porque o fluxo de calor através da placa esquerda aumentou duas vezes.

Na letra (c) queremos a distribuição de temperaturas nas placas, uniforme e em estado estacionário, após um longo período de tempo . No caso 3, então, temos que a perda repentina de líquido refrigerante também ocorre na superfície .

Para esta situação, não há transferência de calor de nenhuma das placas, de modo que, por um período de minutos, , o aquecedor dissipa e depois é desativado. Para determinar a eventual e uniforme distribuição de temperatura no estado estacionário, vamos aplicar a conservação de energia necessária em intervalos de tempo.

A condição inicial corresponde à distribuição de temperatura do Caso 2, e a condição final será uma temperatura uniforme e elevada representando o Caso 3. Usamos como condição de referência para os termos de energia.

Onde,

E a energia elétrica dissipada é:

Para a condição final,

Onde, é a temperatura uniforme final, Caso 3. Para a condição inicial:

Onde, é linear para e constante em para .

Substituindo essa expressão na equação para a condição inicial, temos:

Substituindo os valores:

Voltando ao balanço de energia encontramos

A distribuição de temperatura é mostrada nas coordenadas no passo 2 e identificada como Caso 3. A distribuição é uniforme e consideravelmente superior ao valor máximo para o Caso 2.

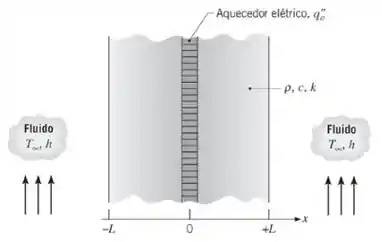
Na letra (d), e última \o/, queremos o histórico da temperatura, nas posições das placas e , ao longo do período transiente entre as distribuições dos Casos 2 e 3. Que é demonstrado nas coordenadas abaixo:

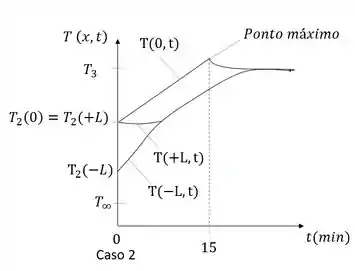
Repara que as temperaturas para os locais no tempo correspondente ao instante em que a superfície se torna adiabática. Essas temperaturas correspondem à distribuição do caso 2. O aquecedor permanece energizado por mais 15 minutos e depois é desativado. A temperatura do ponto médio, é sempre o local mais quente e o valor máximo excede ligeiramente a temperatura final,