Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 91
Considere o elemento combustível revestido do Problema 3.90.
(a) Usando relações apropriadas das Tabelas e , obtenha uma expressão para a distribuição de temperaturas no elemento combustível. Para , , , , e , quais são a maior e a menor temperaturas no elemento combustível, se calor estiver sendo gerado uniformemente a uma taxa volumétrica de ? Quais são as respectivas posições?
(b) Se o isolamento for removido e condições equivalentes de convecção forem mantidas em cada superfície, qual é a forma correspondente da distribuição de temperaturas no elemento combustível? Para as condições da parte (a), quais são a maior e a menor temperaturas no combustível? Quais são as respectivas posições?
(c) Para as condições das partes (a) e (b), represente graficamente as distribuições de temperaturas no elemento combustível.
Passo 1
Fala Galera!!
Nessa questão queremos encontrar (a) a distribuição de temperatura no elemento combustível, com uma superfície isolada e a outra resfriada por convecção. A maior e menor temperatura e locais correspondentes. (b) Igual à parte (a), mas com condições de convecção equivalentes em ambas às superfícies, (c) o gráfico das distribuições de temperatura.
DADOS FORNECIDOS:
Condutividade térmica do combustível:
Condutividade térmica do revestimento:
Coeficiente convectivo:
Metade da espessura do combustível:
Espessura do revestimento:
Temperatura do refrigerante:
Taxa volumétrica de geração de calor:
PRESSUPOSTOS:
(1) Transferência de calor unidimensional;
(2) Estado estacionário;
(3) Geração uniforme;
(4) Propriedades constantes;
(5) Resistência desprezível ao contato.
Passo 2
(a) Podemos desenhar o seguinte esquema para o elemento combustível revestido do Problema 3.90.
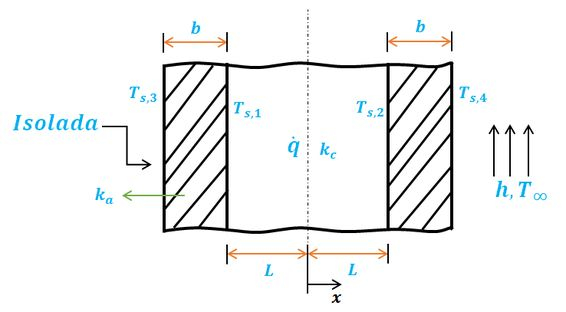
Passo 3
Para resolver essa questão, podemos começar escrevendo e equação da distribuição de temperatura para parede plana da tabela . Temos o seguinte:
Aqui, é a temperatura na direção de , é a taxa de transferência de calor, é a condutividade térmica do combustível, é à distância na direção vertical, e são a temperaturas das superfícies esquerda e direita respectivamente e é comprimento.
Passo 4
Pela tabela podemos encontrar a equação para o fluxo térmica nas superfícies. Para a superfície 1 quando , pela equação temos que o fluxo térmico é o seguinte:
Como o revestimento é isolado em contato com essa superfície é isolado, o fluxo térmico é zero, e, portanto:
Passo 5
Também pela tabela , para a superfície 2 quando , em que conhecemos a temperatura ambiente e coeficiente de transporte, pela equação temos o seguinte:
Aqui, o coeficiente geral de transferência de calor é . Em que:
Passo 6
Agora, vamos colocar e em função dos outros termos para substituir na . Subtraindo a equação 3 da equação 2, temos o seguinte:
Passo 7
Agora, vamos substituir a equação 4 na equação 2. Assim temos:
Passo 8
Agora, vamos substituir as equações 4 e 5 na equação 1. Assim temos:
Substituindo temos o seguinte:
Portanto, a equação de distribuição de temperatura é:
Passo 9
A temperatura máxima ocorre quando
Derivando a equação de destruição de temperatura e igualando a zero, temos:
Portanto a temperatura máxima ocorre quando . Substituindo os dados fornecidos na equação de distribuição de temperatura, temos o seguinte:
Substituindo temos:
Portanto temos que a temperatura máxima é quando .
Passo 10
Devido a equação de distribuição de temperatura ser parabólica e a temperatura máxima ocorrer em , temos então que a temperatura mínima ocorrera em . Substituindo na equação, temos o seguinte:
Portanto temos que a temperatura mínima é quando .
Passo 11
(b) Podemos desenhar o seguinte esquema para o elemento combustível revestido do Problema 3.90 sem isolamento.
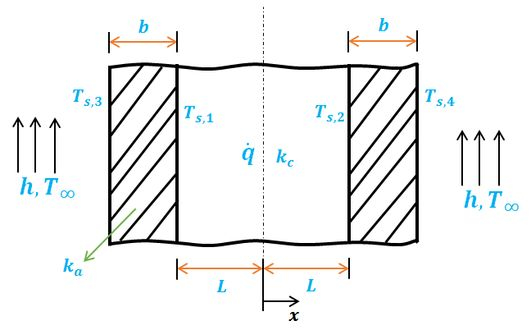
Passo 12
Para resolver essa questão, podemos começar escrevendo e equação da distribuição de temperatura para parede plana da tabela . Temos o seguinte:
Aqui, é a temperatura na direção de , é a taxa de transferência de calor, é a condutividade térmica do combustível, é à distância na direção vertical, e são a temperaturas das superfícies esquerda e direita respectivamente e é comprimento.
Passo 13
Pela tabela , para a superfície 1 quando , em que conhecemos a temperatura ambiente e coeficiente de transporte, pela equação temos o seguinte:
Aqui, o coeficiente geral de transferência de calor é . Em que:
Passo 14
Também pela tabela , para a superfície 2 quando , em que conhecemos a temperatura ambiente e coeficiente de transporte, pela equação temos o seguinte:
Passo 15
Agora, vamos colocar e em função dos outros termos para substituir na . Somando a equação 8 da equação 7, temos o seguinte:
Como é sempre diferente de zero, temos que:
Passo 16
Agora, vamos substituir o que encontramos no passo anterior na equação 8. Assim temos:
Passo 17
Agora, vamos substituir o que encontramos acima e também no passo 15 na equação 6. Assim temos:
Substituindo temos o seguinte:
Portanto, a equação de distribuição de temperatura é:
Passo 18
A temperatura máxima ocorre quando
Derivando a equação de destruição de temperatura e igualando a zero, temos:
Portanto a temperatura máxima ocorre quando . Substituindo os dados fornecidos na equação de distribuição de temperatura, temos o seguinte:
Substituindo temos:
Portanto temos que a temperatura máxima é quando .
Passo 19
Devido a equação de distribuição de temperatura ser parabólica e a temperatura máxima ocorrer em , temos então que a temperatura mínima ocorrera em e . Substituindo na equação, temos o seguinte:
Portanto temos que a temperatura mínima é quando e .
Passo 20
(c) Podemos fazer a seguinte tabela de dados com as equações de distribuição de temperatura encontrada para Letra (a) e a letra (b):
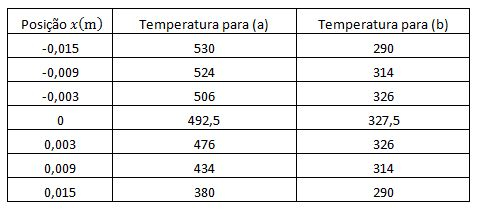
Passo 21
O gráfico da distribuição de temperatura fica da seguinte forma:
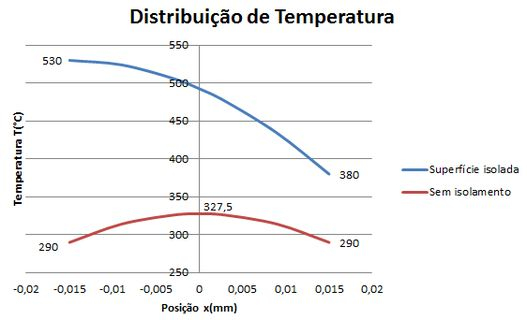
Resposta
(a)
(b)
.