Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 4.Problemas - Ex. 59
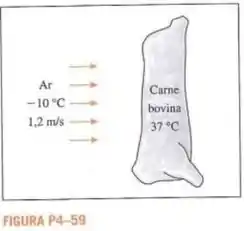
Uma carcaça bovina de , inicialmente a uma temperatura uniforme de , deve ser resfriada com ar refrigerado a fluindo a uma velocidade de . O coeficiente médio de transferência de calor entre a carcaça e o ar é . Trate a carcaça como um cilindro de de diâmetro e de altura e, ignorando a transferência de calor a partir das superfícies da base e do topo, presuma quanto tempo é necessário pra que a temperatura no centro da carcaça diminua para . Além disso, determine se alguma parte da carcaça congelará durante esse processo.
Passo 1
Dados fornecidos:
Diâmetro da carcaça bovina:
A condutividade térmica da carcaça bovina:
Difusividade térmica da carcaça bovina:
Coeficiente médio de transferência de calor:
Temperatura inicial da carcaça bovina:
Temperatura do ar:
Temperatura final no centro da carcaça bovina:
Passo 2
A condução de calor na carcaça é unidimensional na direção radial devido à simetria em torno da linha central.
Vamos começar calculando o número da Biot. Assim temos:
Aqui, é o coeficiente de transferência de calor entre a carcaça e o ar, é o raio externo da carcaça e é a condutividade térmica da carcaça. Substituindo os termos da equação pelos dados fornecidos, temos:
Passo 3
Agora, precisamos determine os coeficientes utilizados na solução aproxima do termo da condução de calor transiente unidimensional para um cilindro com número de Biot usando a fórmula de interpolação.
Para encontrar , podemos interpolar linearmente os valores do coeficiente entre e para obter valor em da tabela 4-2 para um cilindro.
Para encontrar , podemos interpolar linearmente os valores do coeficiente entre e para obter valor em da tabela 4-2 para um cilindro.
Passo 4
Podemos calcular o número de Fourier usando a solução para condução transiente unidimensional em um cilindro submetido a convecção em todas as superfícies. Como estamos interessados no centro do cilindro podemos usar a relação simplifica (4-27). A equação é a seguinte:
Substituindo os termos da equação pelos valores conhecido temos:
Temos que é maior que e, portanto, a solução de um termo é aplicável.
Passo 5
Agora, vamos encontrar o tempo de resfriamento usando a seguinte expressão:
Reescrevendo ela isolando o tempo, temos:
Aqui é a difusividade térmica e é o raio. Substituindo os termos da equação pelos dados conhecido, temos:
Portanto, o tempo é necessário pra que a temperatura no centro da carcaça diminua para é .
Passo 6
A temperatura mais baixa durante o resfriamento ocorrerá na superfície e é determinada como sendo:
Como estamos interessados na superfície, , logo:
Temos também que:
Substituindo na equação, temos:
Podemos encontra o valor de na tabela 4-3. Por meio de interpelação, temos que:
Substituindo os termos pelos dados conhecidos, temos:
Abaixo da temperatura de congelamento de . Portanto, a parte externa da carcaça de carne congelará durante esse processo de resfriamento.