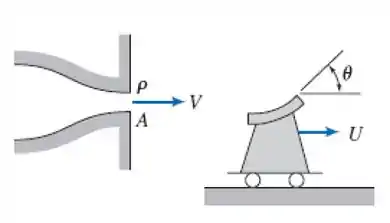
O carrinho com pá defletora do Problema 4.128 se movimenta sem atrito. Ele deve acelerar para a direita. A velocidade do jato é . A área do jato permanece constante em . Desconsidere forças viscosas entre água e a pá. Para o instante em que o carrinho atinge a velocidade , calcule a pressão de estagnação da água saindo do bocal com respeito a um observador fixo, a pressão de estagnação do jato de água saindo do bocal com respeito a um observador sobre o carrinho, a velocidade absoluta do jato saindo da válvula com respeito a um observador fixo e a pressão de estagnação do jato saindo da válvula com respeito a um observador fixo. Como as forças viscosas afetariam a pressão de estagnação do jato, isto é, as forças viscosas aumentariam, diminuiriam ou não alterariam a pressão de estagnação? Justifique sua resposta.

Agora vamos calcular a pressão de estagnação no jato com relação a um observador no carrinho, para isso, devemos considerar a velocidade absoluta, então temos:

Substituindo os valores conhecidos:

Agora vamos calcular a velocidade absoluta do jato saindo da válvula com respeito a um observador fixo. Então, temos:

Substituindo os valores conhecidos (sabendo que o ângulo da pá foi dado no Problema 4.128 e é ), temos:

Agora, calculando o módulo da velocidade, temos:

Agora vamos calcular a pressão de estagnação do jato saindo da válvula com respeito a um observador fixo usando a velocidade absoluta obtida no passo 2: