Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 7.Problemas - Ex. 27

Cem componentes elétricos, cada um dissipando 25   W , estão fixados à superfície de uma placa quadrada de cobre ( 0,2   m   ×   0,2   m ) , e toda a energia dissipada é transferida para a água que se encontra em escoamento paralelo sobre a superfície oposta. Uma protuberância na aresta frontal da placa atua na perturbação da camada-limite e a placa pode ser considerada isotérmica. A velocidade e a temperatura da água são u ∞ = 2   m / s e T ∞ = 17 ° C , e as propriedades termofísicas da água podem ser aproximadas por v = 0,96 × 10 - 6   m 2 / s , k = 0,620   W / ( m · K ) e P r = 5,2 .

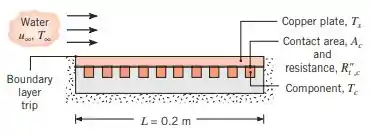
(a) Qual é a temperatura da placa de cobre?

(b) Se cada componente possui uma área superficial de contato com a placa de cobre igual a 1   c m 2 e a resistência térmica de contato correspondente é igual a 2 × 10 - 4   m 2 · K / W , qual é a temperatura dos componentes? Despreze a variação de temperatura ao longo da espessura da placa de cobre.

Passo 1

E aí, beleza?

Vem comigo resolver essa questão!

Vamos lá então!

Letra a)

A equação de taxa de convecção é dada por:

q = h - A T s - T ∞

Sendo:

q = N q c = 100 ⋅ 25 = 2500   W

A = L 2 = 0,02 2 = 0,04   m 2

Calculando R e L :

R e L = u ∞ L v = 2 ⋅ 0,2 0,96 × 10 - 6 = 4,17 × 10 5

Calculando h - :

h - = N u - L k L = 0,037 ⋅ R e L 4 5 P r 1 3 k L

Substituindo os dados:

h - = 0,037 ⋅ 4,17 × 10 5 4 5 ⋅ 5,2 1 3 ⋅ 0,620 0,02 = 6228   W / m 2 ⋅ K

Por fim, calculando a temperatura da placa de cobre:

q = h - A T s - T ∞

2500 = 6228 ⋅ 0,04 ⋅ T s - 17

T s = 27 ° C

Passo 2

Letra b)

Calculando a temperatura dos componentes, despreze a variação de temperatura ao longo da espessura da placa de cobre:

q c = T e - T s R t , c = A R t , c ' ' T e - T s

Substituindo os dados:

25 = 10 - 4 2 × 10 - 4 ⋅ T e - 27

T e = 77 ° C

Bem de boa né?

Até a próxima questão!

Resposta

a )   T s = 27 ° C

b )   T e = 77 ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sobre quais condições a superfície curva pode ser tratada como uma placa plana no escoamento de um fluido e na análise de convecção?
Quais são as vantagens da adimensionalização das equações de convecção?
Considere um escoamento laminar permanente bidimensional sobre placa isotérmica. A espessura da camada limite hidrodinâmica aumenta ou diminui com (a) a distância do bordo de ataque, (b) a velocidade
O escoamento de óleo em um mancal pode ser tratado como escoamento paralelo entre duas grandes placas isotérmicas com uma placa que se desloca a uma velocidade constante de 8 m/s e a outra estacionári
Glicerina a 10°C está fluindo sobre uma placa plana, em velocidade de fluxo livre de 2 m/s. Determine a velocidade e a espessura da camada limite térmica a uma distância de 15c m do bordo de ataque. T