Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 9.Problemas - Ex. 88

Determine a taxa de transferência de calor nas placas de aço do Problema 7.19, levando em conta a convecção natural nas superfícies das placas. Qual é a taxa de variação da temperatura da placa correspondente? Represente graficamente o coeficiente de transferência de calor associado à convecção natural, à convecção forçada e à convecção mista para velocidades do ar variando na faixa 2 ≤ u ∞ ≤ 10   m / s . A velocidade da placa é pequena em comparação com a velocidade do ar.

Passo 1

Opa, tudo bem?

Fica ligado para não se perder e vem comigo resolver essa questão!

Começamos o nosso problema obtendo algumas propriedades dos materiais que utilizaremos.

Tabela A.1 - A ç o   A I S I   1010   ( 573   K ) :

k p = 49,2   W / m ⋅ K

c P = 549   J / k g ⋅ K

ρ = 7832   k g / m 3

Tabela A.4 - A r   ( 433   K ) :

k = 0,0361   W / m ⋅ K

v = 30,4 × 10 - 6   m 2 / s

α = 4,417 × 10 - 5   m 2 / s

P r = 0,688

Bora para os cálculos!

Passo 2

A taxa de transferência de calor inicial da placa é dada pela seguinte equação:

q i = 2 h - A s ( T i - T ∞ )

q i = 2 h - L 2 ( T i - T ∞ )

Mas antes, devemos calcular alguns dados a respeito do nosso problema.

- Calculando o número de Reynolds:

R e L = u ∞ L v = 10 ⋅ 1 30,4 × 10 - 6 = 3,29 × 10 5

R e g i m a   L a m i n a r !

- Calculando o número de Nusselt:

N u - L = N u F = 0,664 R e L 1 2 P r 1 3 = 0,664 ⋅ 3,29 × 10 5 1 2 ⋅ 0,688 1 3 = 336

- Calculando o número de Rayleigh:

R a L = g β ∆ T L 3 v α = 9,8 ⋅ 1 433 ⋅ 300 - 20 ⋅ 1 3 30,4 × 10 - 6 ⋅ 4,417 × 10 - 5 = 4,72 × 10 9

- Pela correlação de Churchill-Chu, temos:

N u - L = N u N = 0,825 + 0,387 R a L 1 6 1 + 0,492 P r 9 16 8 27 2 = 0,825 + 0,387 ⋅ 4,72 × 10 9 1 6 1 + 0,492 0,688 9 16 8 27 2 = 198

Passo 3

Uma vez que os fluxos induzidos por convecção forçada e livre são transversais, temos:

N u - = N u F 3 + N u N 3 1 3 = 336 3 + 198 3 1 3 = 357

Desse modo, temos:

h - = N u - k L = 357 ⋅ 0,0361 1 = 12,9   W / m 2 ⋅ K

Por fim:

q i = 2 h - L 2 ( T i - T ∞ )

q i = 2 ⋅ 12,9 ⋅ 1 2 ⋅ 300 - 20

q i = 7224   W

Passo 4

Aplicando um balanço de energia em um instante no tempo para a placa:

E ´ e n t - E ´ s a i = E ´ a c u m

- E ´ s a i = E ´ a c u m

Abrindo essa equação:

ρ δ L 2 c p d T d t = - h - 2 L 2 T i - T ∞

Isolando d T d t e substituindo os dados:

d T d t = - 2 ⋅ 12,9 ⋅ 300 - 20 7832 ⋅ 0,006 ⋅ 549

d T d t = - 0,28 ° C / s

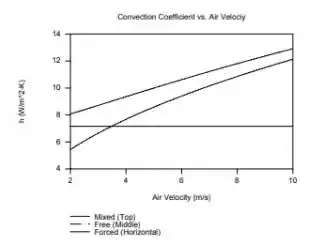
O coeficiente de transferência de calor pode ser avaliado ao longo da faixa de velocidade 2 ≤ u ∞ ≤ 10   m / s , nos fornecendo um gráfico:

Até a próxima questão!

Resposta

q i = 7224   W

d T d t = - 0,28 ° C / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fio elétrico de 3 mm de diâmetro e 12 m de comprimento é envolto com uma cobertura plástica de 1,5 mm de espessura cuja condutividade térmica e emissividade são k = 0,20W / m ⋅ K e ε = 0,9 . Mediçõ
Repita o Prob. 9-44 considerando que a placa de circuito impresso seja colocada horizontalmente com os (a) chips virados para cima e (b) os chips virados para baixo.
Um tanque cilíndrico de propano de 1,5 m de diâmetro e 4 m de comprimento é inicialmente cheio com propano líquido, cuja densidade é 581k g / m 3 . O reservatório é exposto ao ar ambiente a 25 °C, em
A principal força motriz para convecção natural é (a) Força de tensão de cisalhamento(b) Força de empuxo(c) Força de pressão(d) Força de tensão superficial(e) Nenhuma das alternativas anteriores
Os componentes de um sistema eletrônico que dissipa 180 W estão localizados em um duto circular horizontal de 1,2 m de comprimento cujo diâmetro é de 10 cm. Os componentes no duto são refrigerados por