Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas Abrangentes - Ex. 1

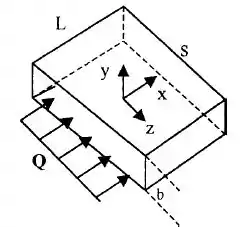
Em uma certa aplicação médica, água à temperatura e pressão ambiente escoa por um canal de seção retangular de comprimento L = 10 cm, largura s = 1 cm e tamanho da folga b = 0,30 mm, como na figura abaixo. A vazão volumétrica é senoidal, com amplitude Q ^ = 0,50   m L / s e frequência f = 20 Hz, isto é, Q = Q ^ s e n ( 2 π f t ) . (a) Calcule Re máximo ( R e = V b / v )   baseado na máxima velocidade média e no tamanho da folga. O escoamento em um canal como esse permanece laminar para Re menor que 2000, aproximadamente. Para número de Re maiores, o escoamento será turbulento. Este escoamento é laminar ou turbulento? (b) Neste problema, a frequência é baixa o suficiente para que, em qualquer instante dado, o escoamento possa ser resolvido como se fosse permanente com a vazão volumétrica correspondente. (Essa é a chamada hipótese quase-permanente) Em qualquer instante de tempo arbitrário, encontre uma expressão para a velocidade do fluxo principal, u, em função de y ,   μ ,   d p / d x e b , em que d p / d x é o gradiente de pressão necessário para manter o escoamento pelo canal com a vazão volumétrica Q. Além disso, estime o valor máximo da componente u da velocidade. (c) Em qualquer instante de tempo, encontre uma relação entre a vazão volumétrica Q e o gradiente de pressão. Sua resposta deve ser dada como uma expressão para Q em função de d p / d x , s ,   b e μ . (d) Calcule a tensão de cisalhamento na parede τ p em função de Q, f, b, s e tempo t. (e) Finalmente, para os números dados no enunciado do problema, calcule a amplitude da tensão de cisalhamento na parede τ p em N/m².

Passo 1

PRIMEIRAMENTE PRA QUÊ UM ENUNCIADO DESSE TAMANHO NÉ? KKKKKK Bem, se você é igual a mim, vamos fazer por partes a questão! Então vamos para a letra (a)!!

Bem, ele quer o Re máximo, certo? Então precisamos encontrar qual é a velocidade máxima!! Só que a velocidade depende da vazão que depende daquela amplitude lá. Bem ele disse que a amplitude é de 0,5 mL/s, certo? Ou seja, esse é o valor máximo de vazão que teremos!!!!!!!!!

Q m á x = 0,5   x   10 - 6     m 3 / s

Q m á x = V m á x A → V m á x = Q m á x b s = 0,5   x   10 - 6 0,0003 0,01 = 0,167   m / s

R e m á x = V m á x b v = 0,167 0,0003 0,001 998 = 50   ( L a m i n a r )

Passo 2

(b) e (c) O estado quase-permanente é dado pelas equações (4.142 – 144) do livro com h = b 2

u = - 1 2 μ d p d x b 2 4 - y 2

u m á x = - 1 2 μ d p d x b 2 4

Q m á x = 2 3 u m á x b s = - s b 3 12 μ d p d x

Passo 3

(d) A tensão de cisalhamento na parede é dada por:

τ w = μ d u d y p a r e d e = b 2 d p d x = 6 μ Q s b 2 = 6 μ Q 0 s b 2 s e n ( 2 π f t )

Passo 4

(e) Para os nossos dados do enunciado, a amplitude da tensão de cisalhamento é igual a:

τ w = μ d u d y p a r e d e = b 2 d p d x = 6 μ Q s b 2 = 6 0,001 0,5   x   10 - 6 0,01 0,0003 2 = 3,3   P a

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No escoamento laminar de um fluido em condutos circulares, o diagrama de velocidades é representado pela equação v = v m a x 1 - r R 2 , onde v m a x é a velocidade no eixo do conduto, R é o raio do c
No tubo da figura, determinar a vazão em volume, em massa, em peso e a velocidade média na seção 2 , sabendo que o fluido é água e que A 1 = 10c m 2 e A 2 = 5c m 2 . ( ρ H 2 O = 1000k g / m 3 , g = 10
Um gás ( γ = 5N / m 3 ) escoa em regime permanente com uma vazão de 5k g / s pela seção A de um conduto retangular de seção constante de 0,5m por 1m . Em uma seção B , o peso específico do gás é 10N /
A água escoa por um conduto que possui dois ramais em derivação. O diâmetro do conduto principal é 15c m e os das derivações são 2,5c m e 5c m , respectivamente. O perfil das velocidades no conduto pr
Um propulsor a jato queima 1k g / s de combustível quando o avião voa à velocidade de 200m / s . Sendo dados ρ a r = 1,2k g / m 3 , ρ g = 0,5k g / m 3 (na seção 2 ), A 1 = 0,3m 2 e A 2 = 0,2m 2 , dete