Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 92

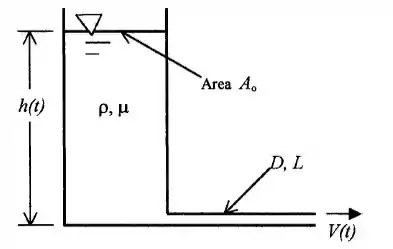
Um tanque de área A0 está sendo drenado em escoamento laminar por um tubo de diâmetro D e comprimento L, como mostra a figura abaixo. Desprezando a energia cinética do jato de saída e supondo que o escoamento no tubo é causado pela pressão hidrostática em sua entrada, deduza uma fórmula para o nível do tanque h(t) se seu nível inicial é h0.

Passo 1

Tudo bem, genteee?!! Então, vamos começar nossas aventuras com a mecânica dos fluidos? O enunciado já falou com a gente que o escoamento é laminar, então podemos já fazer aquela clássica relação de vazão com queda de pressão!!!!

Q s a í d a = π D 4 128 μ Δ p L

Como o tanque vai esvaziar com o tempo, temos um termo de acúmulo associado, certo? Porque se definirmos nosso tanque como um volume de controle fixo, a massa dentro do volume de controle vai estar mudando com o tempo.

Q a c u m u l a d o = d V d t = d A h d t = - A d h d t

O sinal de menos é porque já sabemos que essa derivada será negativa pois estamos DIMINUINDO o nível de água!!

O balanço de massa global diz que o que “entra menos o que sai é igual ao acumulado”, portanto, como não temos entrando nada, ao final, temos que:

Q s a i = Q a c u m u l a d o

Passo 2

Vamos resolver esse problema igualando nossas equações então!!!

π D 4 128 μ Δ p L = - A d h d t

Lembrando que Δ p = ρ g h ( t )

Vamos integrar essa belezinha?

∫ h 0 h d h h = - ∫ 0 t π D 4 ρ g 128 μ L A d t  

Passo 3

Ao final da integração temos o seguinte:

ln ⁡ h h 0 = - π D 4 ρ g 128 μ L A t

h = h 0 exp ⁡ - π D 4 ρ g 128 μ L A t

Resposta

h = h 0 exp ⁡ - π D 4 ρ g 128 μ L A t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os reservatórios da figura são cúbicos. São enchidos pelos tubos, respectivamente, em 100s e 500s . Determinar a velocidade da água na seção A , sabendo que o diâmetro do conduto nessa seção é 1m .
Água é descarregada de um tanque cúbico de 5m de aresta por um tubo de 5c m de diâmetro. A vazão no tubo é 10L / s . Determinar a velocidade de descida da superfície livre da água do tanque e, supondo
Um tubo admite água ( ρ = 1000k g / m 3 ) num reservatório com uma vazão de 20L / s . No mesmo reservatório é trazido óleo ( ρ = 800k g / m 3 ) por outro tubo com uma vazão de 10L / s . A mistura homo
No escoamento turbulento de um fluido em condutos circulares, o diagrama de velocidades é dado pela equação v = v m á x 1 - r R 1 / 7 á , onde todas as grandezas têm o mesmo significado do Exercício 3
Uma torneira enche de água um tanque, cuja capacidade é 6000L , em 1he40m i n . Determinar a vazão em volume, em massa e em peso em unidade do S I se ρ H 2 O = 1000k g / m 3 e g = 10m / s 2 .