Uma ciclista de está andando com sua bicicleta de descendo em uma estrada com inclinação de sem pedalar nem brecar. A ciclista tem uma área frontal de e um coeficiente de arrasto de com o corpo na posição vertical, e uma área frontal de e um coeficiente de arrasto de na posição de corrida. Desprezando a resistência de rodagem e o atrito nos rolamentos, determine a velocidade terminal da ciclista para ambas as posições. Considere a densidade do ar como .
Passo 1
Nossa situação é a seguinte:
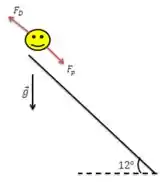
Temos uma ciclista andando por uma rua inclinada. Devemos obter a velocidade terminal da ciclista para as posições vertical e de corrida. Vamos lá?
Para começar, temos que pensar nas forças que agem na ciclista. Como a ciclista não pedala nem breca, as únicas forças são a força peso e a força de arraste.
Fazendo um balanço de forças:
Portanto, para chegar à velocidade terminal,temos que aplicar essa relação para as duas condições.
Passo 2
Começando pela situação em que a ciclista está em posição vertical:
Então:
Passo 3
Pensando agora na situação em que a ciclista está em posição de corrida:
Então, podemos calcular a velocidade terminal:
Resposta
Posição vertical: ;
Posição de corrida: .