Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 45
Um cilindro, de peso específico , flutua num líquido, conforme mostra a figura . Sob a ação de uma força , o cilindro permanece na posição indicada na figura . Determinar os pesos específicos dos líquidos e . Dado: área da base do cilindro .
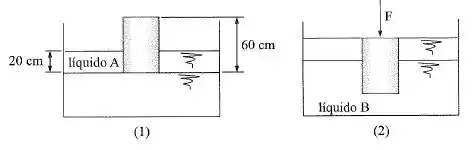
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
No primeiro momento temos que a condição do equilíbrio é que o empuxo provocado pelo líquido é igual ao peso do cilindro:
Sabemos que o empuxo é o produto do peso específico pelo volume submerso. Logo:
Passo 2
No segundo momento temos que o líquido está sofrendo interação de dois líquidos portanto temos a parcela do empuxo de cada líquido. A condição de equilíbrio é de que:
Temos que:
Portanto:
Resposta
Exercícios de Livros Relacionados
O balonismo a ar quente é um esporte popular. De acordo com um artigo recente, “os volumes de ar quente devem ser grandes porque o ar aquecido a 65 ° C acima da temperatura ambiente levanta apenas 0,2
O perfil da seção reta de uma canoa é modelado pela curva y = a x 2 , em que a = 3,89 m–1 e as coordenadas são medidas em pés. Suponha que a largura da canoa tenha valor constante w = 0,6 m em todo o
Quantifique o experimento realizado por Arquimedes para identificar o material da coroa do Rei Hiero. Suponha que você possa medir o peso da coroa do rei no ar, W a , e também o peso na água, W w . Ex
Se a massa M no Problema 3.101 for liberada do tirante, quanto do tirante permanecerá submerso na nova condição de equilíbrio? Qual será a força mínima para cima necessária para levantar a extremidade
Um tanque aberto está cheio com água até o topo. Um recipiente cilíndrico de aço, com espessura de parede δ=1m m , diâmetro externo D=100m m e altura H=1m , é delicadamente colocado dentro d’água com