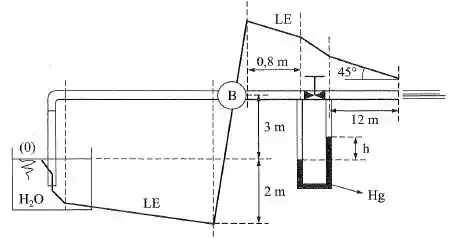
Na instalação da figura, a bomba B recalca uma vazão Q e a LE para tal vazão tem a configuração indicada. A tubulação tem diâmetro constante D = 25m m e o coeficiente de perda de carga f = 0,025 . Sabendo que o manômetro diferencial conectado na válvula V da forma indicada acusa um desnível h = 1m e que g = 10m / s 2 , γ H 2 O = 10 4N / m 3 ; γ H g = 1,3.10 5N / m 3 , determinar:a) a vazão Q;b) a potência no eixo da bomba, supondo um rendimento de 59%.

Q = 2,2.10 - 3m 3 / s N B = 1260,3W

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 22

Na instalação da figura, a bomba B recalca uma vazão Q e a LE para tal vazão tem a configuração indicada. A tubulação tem diâmetro constante e o coeficiente de perda de carga . Sabendo que o manômetro diferencial conectado na válvula V da forma indicada acusa um desnível e que , ; , determinar:

a) a vazão Q;

b) a potência no eixo da bomba, supondo um rendimento de 59%.

Passo 1

Tá legal, a primeira coisa que vamos fazer é notar que como o manômetro conectado na válvula indica uma diferença de nível de 1 m, que é a perda de carga no trecho, podemos usar trigonometria na figura para escrever

Isolando da equação acima e substituindo os valores conhecidos, temos:

Com isso podemos encontrar a vazão do sistema:

Passo 2

Agora para encontrar a potência no eixo da bomba, precisamos encontrar o valor da sua carga, e para isso, vamos aplicar o equilíbrio de energia entre os pontos 0 e 5 (saída da tubulação)

Substituindo os valores conhecidos:

Então precisamos encontrar a perda de carga total no sistema, para isso, vamos separar o sistema em trechos menores e encontrar as perdas em cada um deles, e depois somaremos esses valores para encontrar a perda total.

Passo 3

Aplicando o equilíbrio de energia entre os pontos 0 e 1 (pouco antes da bomba), temos:

Substituindo os valores conhecidos:

Agora para os pontos 2 e 3, saída da bomba e chegada na válvula V, temos somente perda de carga distribuída, então podemos escrever:

E, para calcular a perda de carga entre os pontos 3 e 4, na válvula, vamos aplicar o equilíbrio manométrico para o manômetro instalado na válvula:

Substituindo os valores conhecidos:

E essa diferença é justamente a perda de carga no trecho 3-4. Agora, para encontrar a perda de carga no trecho 4 – 5, vamos usar a relação trigonométrica escrita no passo 1, onde:

Então, a perda de carga total será:

Passo 4

Agora podemos voltar à equação da carga da bomba escrita no passo 2:

E, com isso, podemos aplicar a equação para a potência da bomba, que é dada por:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um difusor cônico, com 150 mm de comprimento, é usado para expandir um tubo de um diâmetro de 50 mm para um diâmetro de 89 mm. Para uma vazão de água de 47 L/s, estime o aumento na pressão estática. Q

Encontrou-se espaço para a instalação de um difusor cônico, com comprimento de 0,45 m, no sistema de ventilação da sala limpa descrito no Problema 8.106. O melhor difusor com este comprimento deve ser

Água é descarregada para a atmosfera a partir de um grande tanque, em regime permanente e através de um trecho de tubo de plástico liso. O diâmetro interno do tubo é 3,18 mm e seu comprimento é 15,3 m

Um difusor cônico é usado para expandir um tubo de um diâmetro de 100 mm para um diâmetro de 150 mm. Determine o comprimento mínimo do difusor, se desejamos um coeficiente de perda (a) K d i f u s o r

Analise o escoamento através de uma expansão súbita para obter uma expressão para a velocidade média V - 1 em termos da variação de pressão ∆ p = p 2 - p 1 , da razão de áreas R A , da massa específic