Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 97

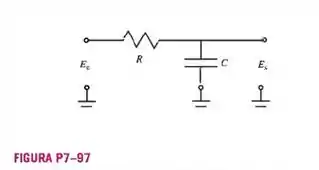
Em muitos circuitos elétricos nos quais algum tipo de escala de tempo está envolvido, como filtros e circuitos de temporizaçào (Figura— um filtro passa baixo), você pode ver um resistor (R) e um capacitor (C) em série. Na verdade, o produto de R e C é chamado de constante de tempo elétrica, RC. Mostrando todo o seu trabalho, quais são as dimensões primárias de RC. Usando apenas argumentação dimensional, explique por que um resistor e um capacitor quase sempre estão juntos em circuitos temporizadores.

Passo 1

Vamos fazer o seguinte, galera, vamos destrinchar todos os parâmetros que a gente ver pela frente, até chegar a um parâmetro que possa ser escrito por uma dimensão primária! Beleza?

R C = R e s i s t ê n c i a × C a p a c i t â n c i a  

Vamos primeiro focar na resistência:

R e s i s t ê n c i a = t e n s ã o × c o r r e n t e

Para achar as dimensões de resistência, vamos ver as de tensão:

t e n s ã o = e n e r g i a c a r g a

Energia:

e n e r g i a = m a s s a × v e l o c i d a d e 2 2

e n e r g i a = { m 1 L 2 s - 2 }

Carga:

c a r g a = c o r r e n t e × t e m p o

c a r g a = { I 1 t 1 }

Agora podemos achar as dimensões de tensão:

t e n s ã o = m 1 L 2 t - 2 × I 1 t 1 - 1 = { m 1 L 2 t - 3 I - 1 }

Agora para achar as dimensões primárias de resistência só falta dimensionar corrente e corrente tem apenas uma dimensão primária!!!

c o r r e n t e = { I 1 }

Agora dimensionando resistência:

R e s i s t ê n c i a = m 1 L 2 t - 3 I - 1 × I 1 - 1 = m 1 L 2 t - 3 I - 2

Passo 2

Agora falta as dimensões de capacitância! Por sorte a gente terminou de resolver no exercício anterior!

C = I 2 t 4 m - 1 L - 2

Passo 3

Agora vamos juntar o que achamos até aqui para achar as dimensões primárias de R C :

R C = m 1 L 2 t - 3 I - 2 × I 2 t 4 m - 1 L - 2 = { t }

Como a gente pode ver a dimensão primária de R C é tempo, isso explica porque um resistor e um capacitor em série quase sempre estão juntos em circuitos temporizadores.

Resposta

As dimensões primárias de R C :

R C = m 1 L 2 t - 3 I - 2 × I 2 t 4 m - 1 L - 2 = { t }

Como a gente pode ver a dimensão primária de R C é tempo, isso explica porque um resistor e um capacitor em série quase sempre estão juntos em circuitos temporizadores.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Foi sugerido, no projeto de um “sprinkler” agrícola, que um elemento estrutural fosse mantido fixo por meio de um arame esticado ao longo da linha de centro de um tubo; acreditava-se que um arame rela
Para um escoamento pressurizado, em regime permanente e completamente desenvolvido de um fluido incompressível através de um canal retilíneo de comprimento L, podemos definir a resistência hidráulica
7.65 Ascaracterísticasfluidodinâmicasdeumaboladegolfedevemsertestadasusandoummodeloemumtúneldevento.Os parâmetrosdependentessãoaforçadearrasto,FD,eaforçadesustentação,FL,sobreabola.Osparâmetrosindepen
7.68Ummodelodehidrofóliodevesertestadoemescalade1:20.AvelocidadedetesteescolhidadevereproduzironúmerodeFroude correspondenteàvelocidadedoprotótipode30m/s.Paramodelaracavitaçãocorretamente,oíndicedecav
7.55 Osprojetistasdeumgrandebalão,queoperaráancoradoparacoletadeamostraseanálisedepoluiçãoatmosférica,desejamsaber quearrastohaverásobreobalãoparaumavelocidademáximadeventoadmitidade5m/s(oaréconsidera