Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 14
Cite pelo menos três outros nomes para a derivada material e escreva uma breve explicação sobre o motivo pelo qual cada nome é apropriado.
Passo 1
O enunciado quer que a gente explique os diversos nomes que a derivada material possui. O primeiro passo para fazer essa explicação é entender o que é a derivada material. Essa derivada é representada pelo símbolo (onde é o tempo). Essa derivada é igual à derivada total usada na matemática. Ou seja, ela é a taxa de variação de uma propriedade do fluido com o tempo .
Então vamos imaginar um exemplo. Imagine água escoando através do rio. No ponto A desse rio passa uma partícula de água a todo instante com uma velocidade que varia com o tempo . Essa mesma partícula passa com uma velocidade diferente pelo ponto B. Isso significa que a velocidade é uma propriedade da água varia com a posição da partícula (coordenadas , e ) e com o tempo.
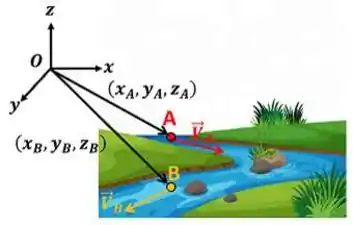
Logo a derivada total dessa velocidade pode ser calculada através da regra da cadeia.
Além disso, a taxa de variação da posição da partícula é a componente da velocidade da partícula no eixo . O mesmo vale para a taxa de variação da posição da partícula e a taxa de variação da posição da partícula . Ou seja, é a componente da velocidade no eixo e é a componente da velocidade no eixo .
Substitundo essa informação na equação:
Onde é a componente da velocidade no eixo , é a componente da velocidade no eixo e é a componente da velocidade no eixo .
Essa derivada total de pode ser chamada de derivada material. Essa derivada material é representada com um maiúsculo.
Passo 2
Vimos pelo exemplo acima que a derivada material pode ser chamada de derivada total, porque ela é a soma das taxas de variação da propriedade (no caso do exemplo, a propriedade é a velocidade ) com relação a todas as variáveis de que ela depende. Exemplificando: a derivada material da velocidade é a soma das taxas de variação da velocidade em relação a , , e .
Passo 3
Vimos através do exemplo da partícula de água escoando pelo rio que a derivada material da velocidade da água pode ser entendida como a taxa de variação da velocidade dessa partícula conforme ela atravessa o rio. Como é a taxa de variação de uma propriedade da partícula de fluido, ela também pode ser chamada de derivada de partícula.
Passo 4
Como foi dito, conseguimos ver através do exemplo da partícula de água escoando pelo rio que a derivada material da velocidade da água pode ser entendida como a taxa de variação da velocidade dessa partícula conforme ela atravessa o rio.
No entanto, acompanhar uma partícula de fluido escoando pelo rio é muito difícil. Para facilitar os nossos estudos, ao invés de monitorar as propriedades de uma partícula passando por vários pontos, monitoramos as propriedades das partículas que passam por um ponto.
Exemplificando: ao invés da gente monitorar a velocidade , da partícula que passa pelos pontos A, B e C do rio, monitoramos a velocidade das partículas que passam por um único ponto A. Podemos fazer esse monitoramento ponto a ponto do rio.
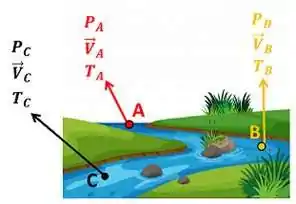
A fórmula da taxa de variação é usada para transformar a forma mais difícil de se estudar um escoamento (seguindo cada partícula de fluido) na forma mais fácil de se estudar um escoamento (monitorando o escoamento ponto a ponto).
Quando estudamos o movimento do fluido acompanhando e monitorando suas partículas, estamos estudando o escoamento do fluido através de uma abordagem chamada de lagrangiana!
Ou seja, a derivada material de uma propriedade do fluido serve para transformar a abordagem lagrangiana (mais difícil) na abordagem de monitoramento ponto a ponto. Por isso ela pode ser chamada de derivada lagrangiana.
Pronto! Explicamos os três nomes mais importantes da derivada material .
Resposta
Derivada total, porque ela é a soma das taxas de variação da propriedade com relação a todas as variáveis independentes. Derivada de partícula, porque ela é a taxa de variação da propriedade de uma partícula de fluido que escoa pelo rio. Derivada lagrangiana, porque essa derivada é usada para transformar a abordagem lagrangiana em uma equação baseada em abordagem mais fácil.