Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 5.Problemas - Ex. 36

Em climas frios, os tubos de água podem congelar e estourar se não forem tomadas medidas preventivas. Nesse caso a parte exposta de um tubo no solo se rompe, e a água sobe até 34   m . Estime a pressão manométrica da água no tubo. Siga as suas hipóteses e discuta se a pressão real é maior ou menos do que o valor que você previu.

Passo 1

Temos que nosso problema aqui envolve a conversão de fluxo, energia cinética e potencial entre si, sem envolver bombas, turbinas e componentes desnecessários com grandes perdas por atrito, e, portanto, é adequado para o uso da equação de Bernoulli.

Passo 2

A altura da água será máxima de acordo com as premissas declaradas.

Iremos adotar que a velocidade dentro da mangueira é relativamente baixa ( V 1   ≅   0 ) e consideramos a seção de ruptura do tubo como o nível de referência ( z 1   =   0 ) .

No topo da trajetória da água, V 2   =   0 . Como na figura abaixo...

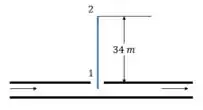
Então aplicando equação de Bernoulli, teremos que:

P 1 ρ g + V 1 2 2 g + z 1 = P 2 ρ g + V 2 2 2 g + z 2

P 1 ρ g = P a t m ρ g + z 2

P 1 - P a t m ρ g = z 2

P 1 m a n o m é t r i c a ρ g = z 2

Passo 3

Agora, adotando ρ = 1000   k g / m 3 e resolvendo para P 1 m a n o m é t r i c a ...

P 1 m a n o m é t r i c a = ρ g z 2 = 1000 k g m 3 9,81 m s 2 34   m 1   k P a 1 k N m 2 1   k N 1000 k g ∙ m s 2 = 334   k P a

Portanto, a pressão principal deve estar pelo menos 334   k P a acima da pressão atmosférica.

Resposta

Temos que a pressão manométrica será de:

P 1 m a n o m é t r i c a = 334   k P a

Portanto, a pressão principal deve estar pelo menos 334   k P a acima da pressão atmosférica.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a velocidade de aproximação não for alta demais, uma saliência no fundo de um canal d’água causará um afundamento ∆ h do nível da água, que pode servir para medição de vazão. Se, como mostra a Figu
Na Figura P3.174, o pistão desloca água a 20°C. Desprezando as perdas, calcule a velocidade na saída, V 2 , em m/s. Se D 2 for diminuído ainda mais, qual será o máximo valor possível de V 2 ?
A bomba da Figura P3.183 bombeia gasolina a 20°C de um reservatório. As bombas são muito prejudicadas se o líquido vaporizar (cavitar) antes de entrar na bomba. (a) Desprezando as perdas e considerand
O escoamento sobre o vertedouro da Figura P3.176 é considerado uniforme e hidrostático nas seções 1 e 2. Se as perdas são desprezadas, calcule (a) V 2 e (b) a força por unidade de largura da água sobr
Um tanque cilíndrico de diâmetro D contém líquido a uma altura inicial h 0 . No tempo t = 0 , um pequeno tampão de diâmetro d é removido do fundo. Usando a equação de Bernoulli sem perdas, deduza (a)