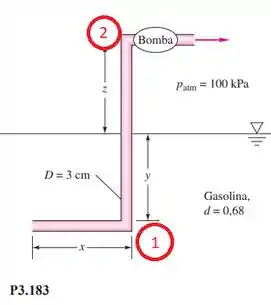
A bomba da Figura P3.183 bombeia gasolina a 20°C de um reservatório. As bombas são muito prejudicadas se o líquido vaporizar (cavitar) antes de entrar na bomba. (a) Desprezando as perdas e considerando que a vazão é de 246 L/min, encontre as limitações em (x, y, z) para evitar a cavitação. (b) Se forem incluídas as perdas por atrito no tubo, que limitações adicionais podem ser importantes?

Nesta questão vamos precisar analisar a partir do momento em que existe a diferença de altura, sendo assim, vamos aplicar Bernoulli nos pontos a seguir:

Como o diâmetro é o mesmo por toda a tubulação, a área da seção transversal também será a mesma, sendo assim, pela equação da continuidade a velocidade será a mesma por todo o escoamento (considerando a vazão constante). Sabemos que , logo:

A pressão em 1 será igual a pressão atmosférica mais a pressão hidrostática da gasolina, ou seja:

Já é a pressão de vapor da gasolina a 20°C, que pela tabela A3, é .

Se quisermos evitar a cavitação, basta que z seja menor que 6,73 m.

Se forem incluídas perdas por atrito no tubo basta fazer com que o comprimento total do tubo () seja maior que as perdas por atrito;