Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 175

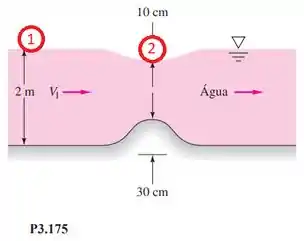
Se a velocidade de aproximação não for alta demais, uma saliência no fundo de um canal d’água causará um afundamento ∆ h do nível da água, que pode servir para medição de vazão. Se, como mostra a Figura P3.175, ∆ h = 10   c m quando a saliência tiver 30 cm de altura, qual será a vazão volumétrica Q por unidade de largura, desprezando as perdas? Em geral, ∆ h será proporcional a Q?

Passo 1

Para este problema vamos aplicar Bernoulli entre os pontos 1 e 2, representados na figura abaixo:

Como ambos os pontos possuem p = p a t m , a diferença de pressão será zero, sendo assim:

p 1 + ρ 2 V 1 2 + ρ g z 1 = p 2 + ρ 2 V 2 2 + ρ g z 2

p a t m + ρ 2 V 1 2 + ρ g z 1 = p a t m + ρ 2 V 2 2 + ρ g z 2

V 1 2 2 + g h 1 = V 2 2 2 + g ( 0,3 + h 2 )

Onde h 2 é o nível da água acima da saliência e 0,3 m a altura da saliência.

Pela equação da continuidade:

V 1 h 1 = V 2 h 2

V 2 = V 1 h 1 h 2

Então:

V 1 2 2 + g h 1 = V 1 2 * h 1 h 2 2 2 + g ( 0,3 + h 2 )

V 1 2 2 h 1 h 2 2 - 1 = g ( h 1 - 0,3 - h 2 )

O termo h 1 - 0,3 - h 2 é o nível do afundamento, ou seja, h 1 - 0,3 - h 2 = ∆ h :

V 1 2 = 2 g ∆ h h 1 h 2 2 - 1

Como V 1 é diretamente proporcional a Q 1 , podemos ver pela expressão acima que ∆ h não é diretamente proporcional à Q 1 e sim proporcional ao quadrado de Q 1 .

Passo 2

Terminando de isolar a velocidade em 1:

V 1 = 2 g ∆ h h 1 h 2 2 - 1

Quando ∆ h = 0,1   m :

h 1 - 0,3 - h 2 = ∆ h

2 - 0,3 - h 2 = 0,1

h 2 = 1,6   m

E a velocidade em 1:

V 1 = 2 * 9,81 * 0,1 2 1,6 2 - 1 = 1,87 m s

Logo, a vazão volumétrica por largura será:

Q = V * h = V 1 * h 1 = 1,87 * 2 = 3,74 m 3 s * m

Resposta

Q = 3,74 m 3 s * m

∆ h é proporcional ao quadrado de Q 1 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a turbina extraindo energia através de um conduto forçado em uma barragem, como na Figura P3.132. Para escoamento turbulento em dutos (Capítulo 6), a perda de carga por atrito é aproximadame
A bomba da Figura P3.144 cria um jato d’água a 20 ° C, orientado para atingir uma distância horizontal máxima. As perdas por atrito do sistema são de 6,5 m. O jato pode ser aproximado pela trajetória
Repita o Problema P3.49, considerando que p1 seja desconhecida e usando a equação de Bernoulli (sem perdas). Calcule a nova força sobre os parafusos com essa hipótese. Qual é a perda de carga entre 1
O sistema bomba-turbina da Figura P3.135 retira água do reservatório superior durante o dia para produzir energia elétrica para uma cidade. À noite, o sistema bombeia água do reservatório inferior par
Um barco anti-incêndio retira água do mar (d = 1,025) por um tubo submerso e a descarrega através de um bocal, como na Figura P3.137. A perda de carga total é de 2 m. Se a eficiência da bomba é de 75%