Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 11.Problemas - Ex. 21

O coeficiente de arrasto de um carro nas condições de projeto de 1   a t m ,   25 ° C e 90   k m / h deve ser determinado experimentalmente em um grande túnel de vento em um teste de escala total. A altura e largura do carro são 1,40   m e 1,65   m , respectivamente. Se a medida da força horizontal agindo sobre o carro foi de 300   N , determine o coeficiente de arrasto total desse carro.

Passo 1

Vamos começar desenhando a nossa situação:

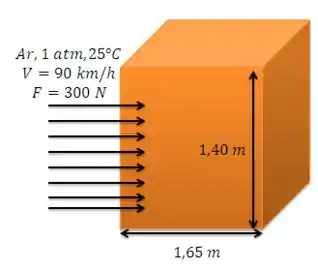
Temos ar escoando sobre um carro de área projetada 1,40   m × 1,65   m . Sabemos que a força exercida pelo ar é de F = 300   N quando a velocidade de corrente é V = 90   k m / h . Além disso, o ar está em condições ambientes P = 1   a t m e T = 25 ° C .

A partir destes dados devemos obter o coeficiente de arrasto. Vamos lá?

Passo 2

Para isso, vamos primeiro encontrar as propriedades do ar nestas condições. De acordo com a Tabela A - 9 do apêndice:

ρ = 1,184   k g / m 3

Para obter o coeficiente de arrasto podemos aplicar a relação:

F D = C D A p ρ V 2 2

2 F D = C D A p ρ V 2

C D = 2 F D A p ρ V 2

Passo 3

Substituindo os valores fornecidos no enunciado:

C D = 2 × 300 1,40 × 1,65 × 1,184 × 90 3,6 2

C D = 2 × 300 1,40 × 1,65 × 1,184 × 25 2

C D = 0,351

Resposta

O coeficiente de arrasto nestas condições é C D = 0,351 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Admita que o avião do Problema 7.116 seja equipado com todos os melhores dispositivos de alta sustentação da Figura 7.28. Qual a sua mínima velocidade de estol em km/h? Calcule a distância de parada s
Na época anterior à guerra, havia uma controvérsia, talvez apócrifa, sobre se o abelhão (também conhecido como mamangaba) teria uma aerodinâmica apropriada para voar. O abelhão B o m b u st e r r e s
Mostre que, se as Equações ( 7.70 ) e ( 7.71 ) são válidas, a razão máxima entre a sustentação e o arrasto ocorre quando C A = 2 C A ∞ . Quais são F S / F A m á x á e a para uma asa simétrica quando R
Em 2001, um avião comercial perdeu toda a potência durante um voo a 10.000m sobre o Oceano Atlântico, a cerca de 100k m da Ilha dos Açores. Os pilotos, com habilidade admirável, colocaram o avião em u
O abelhão pode ficar suspenso no ar à velocidade igual a zero, batendo as asas. Usando os dados do Problema7.123 , conceba uma teoria para asas móveis, em que a batida descendente seja modelada como u