Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 40

Coeficientes de transferência de calor por convecção para uma superfície horizontal aquecida voltada para cima podem ser determinados por um sensor cujas características específicas dependem se a temperatura da vizinhança é conhecida. Para a configuração A, um disco de cobre, que é eletricamente aquecido na parte inferior, é encaixado em um material isolante de modo que todo o calor é transferido por convecção e radiação na superfície superior. Se a emissividade da superfície e as temperaturas do ar e da vizinhança forem conhecidas, o coeficiente convectivo pode ser determinado a partir de medidas da potência elétrica e da temperatura superficial do disco. A configuração B é usada em situações nas quais a temperatura da vizinhança não é conhecida. Uma fina fita isolante separa discos semicirculares com aquecedores elétricos independentes e diferentes emissividades. Se as emissividades e a temperatura do ar forem conhecidas, o coeficiente convectivo pode ser determinado a partir de medidas da potência elétrica fornecida para cada disco para mantê-los a uma mesma temperatura.

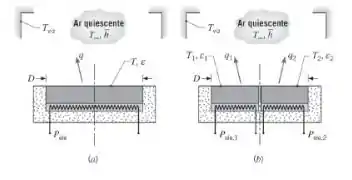
  1. Em uma aplicação da configuração A, com um disco com diâmetro D = 160 mm e emissividade ε = 0,8, valores de Pele = 10,8 W e T = 67°C são medidos para T∞ = Tviz = 27°C. Qual é o valor correspondente do coeficiente convectivo médio? Como ele se compara às previsões baseadas em correlações-padrão?
  2. Agora considere uma aplicação com a configuração B na qual T∞ = 17°C e Tviz não é conhecida. Com D = 160 mm, ε1 = 0,8 e ε2 = 0,1; valores de Pele,1 = 9,70 W e Pele,2 = 5,67 W são medidos quando T1 = T2 = 77°C. Determine o valor correspondente do coeficiente convectivo e a temperatura da vizinhança. Como o coeficiente convectivo se compara às previsões com uma correlação apropriada?

Passo 1

Fala aí! Vamos fixar nossos conhecimentos resolvendo esse probleminha? Vamos nessa!

O enunciado quer que a gente responda essas letras aí… Então vamos nessa!

Mas antes precisaremos de dados adicionais para o nosso cálculo, vamos encontrar eles no apêndice do livro, tabela A-4, assumindo um T f = 320   K :

k = 0,0278   W / m . K v = 17,9   .   10 - 6   m ² / s α = 25,5   .   10 - 6   m ² / s

β = 3,13   .   10 - 3   K - 1 P r = 0,704

Vamos as continhas então!

Passo 2

Para resolver a letra a, e encontrar o h _ m é d i o e comparar

com o esperado, vamos então:

q = q c o n v + q r a d = P e l e c

h _ = P e l e c - ε   .   σ   .   A s   .   T 4 - T s u r 4 A s   .   T - T ∞

h _ = 10,8   -   0,8   .   5,67   .   10 - 8   .   π   .   0,16 ² 4   .   340 4 - 300 4 π   .   0,16 ² 4   .   40

h _ = 7,46   W / m ² . K

Agora vamos fazer a comparação… Precisamos saber alguns fatores antes, como o R a L :

R a L = g   .   β   .   T s - T ∞   .   L ³ v   .   α

Mas nós não temos o L , vamos achar ele:

L = A s P

L = D 4

L = 0,16 4

L = 0,04   m

Agora sim, voltaremos a equação ali de cima:

R a L = 9,8   .   3,13   .   10 - 3   .   77 - 24   .   ( 0,04 ) ³ 17,9   .   10 - 6   .   25,5   .   10 - 6

R a L = 1,72   .   10 5

E por fim teremos o nosso h _ :

h _ = k L .   0,54   .   R a L 1 / 4

h _ = 0,0278 0,04 .   0,54   .   1,72   .   10 5 1 / 4

h _ = 7,64   W / m ² . K

Concluímos que os valores são muito próximo, né?

Vamos para a próxima parte então!

Passo 3

A letra b, vamos calcular a temperatura e os coeficientes convectivos para comparação!

Vamos começar separando essas equações aqui:

P e l e c ,   1 = q c o n v ,   1 + ε 1   .   σ   .   A s 2   .   T 4 - T s u r 4

P e l e c ,   2 = q c o n v ,   2 + ε 2   .   σ   .   A s 2   .   T 4 - T s u r 4

E com essa relação:

q c o n v ,   1 = q c o n v ,   2

Vamos ter:

T s u r = T 4 - P e l e c ,   1 - P e l e c ,   2 ε 1 - ε 2   .   σ   .   A s 2 1 / 4

T s u r = 350 4 - 4,03 0,7   .   5,67   .   10 - 8   .   0,02 2 1 / 4

T s u r = 264   K

Passo 4

Agora os coeficientes convectivos para comparação:

h _ = P e l e c - ε 1   .   σ   .   A s / 2 .   T 4 - T s u r 4 A s / 2   .   T - T ∞

h _ = 9,70   -   0,8   .   5,67   .   10 - 8   .   π   .   0,16 ² 4 / 2 .   340 4 - 300 4 π   .   0,16 ² 4 / 2   .   40

h _ = 8,49   W / m ² . K

Agora vamos fazer a comparação… Sendo agora o nosso R a L :

R a L = 2,58   .   10 5

Vamos ter nosso h _ :

h _ = k L .   0,54   .   R a L 1 / 4

h _ = 0,0278 0,04 .   0,54   .   2,58   .   10 5 1 / 4

h _ = 8,46   W / m ² . K

Que é muito parecido com o outro que encontramos!

Uhul! Conseguimos!!

Resposta

  1. h _ = 7,46   W / m ² . K e h _ = 7,64   W / m ² . K

  2. T s u r = 264   K h _ = 8,49   W / m ² . K e h _ = 8,46   W / m ² . K
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma superfície vertical quente com 15 cm de largura e 18 cm de altura no ar 20°C deve ser resfriada por um dissipador de calor com aletas igualmente espaçadas de perfil retangular. As aletas têm 0,1 c
Uma vareta de 5 cm de diâmetro com temperatura de superfície de 100°C é submersa em um banho de líquido. Determine os números de Grashof e Rayleigh se o fluido é:Água (20°C); Amônia Líquida (20°C);Óle
Considere uma janela de painel duplo composta por duas folhas de vidro separadas por um espaço de ar de 1 cm de largura. Alguém sugere a inserção de uma fina folha de vinil no meio dos dois vidros par
Alguém alega que o espaço de ar em uma janela de painel duplo reforça a transferência de calor da casa por causa das correntes de convecção natural que ocorrem no espaço de ar e, por isso, recomenda q
Duas esferas concêntricas com diâmetros de 15 cm e 25 cm ão separadas por ar a 1 atm de pressão. As temperaturas da superfície das duas superfícies aprisionando o ar são T 1 = 350K e T 2 = 275K , resp