Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 47

Placas de circuitos integrados (CI) são colocadas no interior de um duto e dissipam um total de 500 W. O duto tem uma seção transversal quadrada com w = H = 150 mm e um comprimento de 0,5 m. O ar entra no duto a 25°C e 1,2 m3 /min, e o coeficiente convectivo entre o ar e as superfícies internas do duto é de hi = 50 W/(m2 · K). Toda a superfície externa do duto, que é anodizada com uma emissividade de 0,5, está exposta ao ar ambiente e a uma grande vizinhança a 25°C.

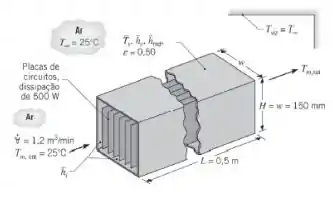
A sua tarefa é desenvolver um modelo para estimar a temperatura de saída do ar, Tm,sai , e a temperatura média da superfície do duto, Ts .

  1. Supondo uma temperatura na superfície de 37°C, estime o coeficiente de transferência de calor por convecção natural médio, he, na superfície externa do duto.
  2. Supondo uma temperatura na superfície de 37°C, estime o coeficiente de radiação linearizado médio, hrad, na superfície externa do duto.
  3. Efetue um balanço de energia no duto considerando a dissipação de potência elétrica nos CIs, a taxa de variação da energia do ar escoando através do duto e a taxa de transferência de calor do ar no interior do duto para a vizinhança. Expresse o último processo em termos das resistências térmicas entre a temperatura média do ar no duto, Tm , e a temperatura do ar ambiente e da vizinhança.
  4. Substitua os valores numéricos na expressão da parte (c) e calcule a temperatura do ar na saída, Tm,sai . Estime o valor correspondente de s. Comente os seus resultados e as hipóteses inerentes ao seu modelo

Passo 1

Fala aí! Vamos fixar nossos conhecimentos resolvendo esse probleminha? Vamos nessa!

O enunciado quer que a gente encontre a solução dessas quatro letrinhas… Então vamos nessa!

Mas antes precisaremos de dados adicionais para o nosso cálculo, vamos encontrar eles no apêndice do livro, tabela A-4, assumindo um T f = T _ s + T ∞ / 2 :

k = 0,0266   W / m . K v = 1,629   .   10 - 5   m ² / s P r = 0,706

α = 2,309   .   10 - 5   m ² / s β = 0,003289   K - 1 ρ = 1,148   k g / m ³

c p = 1007   J / k g . K

Vamos as continhas então!

Passo 2

Para resolver a letra a, precisamos usar a relação:

h _ e v ,   o = 2 .   h _ v   +   h _ t   +   h _ b 4

Temos que encontrar esse três caras que não conhecemos, vamos começar com o h _ v :

h _ v = N u _ L   .   k H

E vamos encontrar o N u _ L assim olha:

N u _ L = 0,68 + 0,670   .   R a L 1 / 4 1 + 0,492 P r 9 / 16 4 / 9

Precisamos encontrar esse valor de R a L :

R a L = g   .   β   .   T _ s + T ∞   .   H 3 v   .   α

R a L = 9,8   .   0,003289   .   37 + 25   .   0,150 3 1,629   .   10 - 5   .   2,309   .   10 - 5

R a L = 3,47   .   10 6

Beleza! Vamos achar o N u _ L :

N u _ L = 0,68 + 0,670   .   3,47   .   10 6 1 / 4 1 + 0,492 0,706 9 / 16 4 / 9

N u _ L = 22,9

E enfim encontramos que:

h _ v = 22,9   .   0,0266 0,150

h _ v = 4,05   W / m ² . K

Passo 3

Agora vamos achar o h _ t :

h _ t = 0,54   .   R a L 1 / 4

h _ t = 0,54   .   3,47   .   10 6 1 / 4

h _ t = 5,25   W / m ² . K

E o h _ b :

h _ b = 0,52   .   R a L 1 / 5

h _ b = 0,52   .   3,47   .   10 6 1 / 5

h _ b = 2,75   W / m ² . K

E enfim teremos:

h _ e v ,   o = 2 .   4,05   +   5,25   +   2,75 4

h _ e v ,   o = 4,03   W / m ² . K

Passo 4

Agora vamos para a letra b, precisamos achar o seguinte:

h _ r a d = ε   .   σ   .   T _ s + T s u r   .   T _ s ² + T s u r ²

h _ r a d = 0,5   .   5,67   .   10 - 8   .   310 + 298   .   310 ² + 298 ²

h _ r a d = 3,2   W / m ² . K

Show! Partiu letra c!

Passo 5

Para resolver essa vamos começar com um balanço de energia:

E e n t r a d a - E s a í d a + E g e r a ç ã o = 0

- q a d v + P e l e c - q s a í d a = 0

Bom, esse nosso q a d v pode ser calculado assim:

q a d v = m   .   c p   .   T m ,   o - T m ,   i

E o q s a í d a que é exatamente o que a letra c quer, vai ficar assim:

q s a í d a = T _ m   -   T ∞ R e v ,   e n t r a d a     +     1 R e v ,   s a í d a + 1 R r a d - 1

Não podemos esquecer que o nosso T _ m = T m ,   e n t r a d a + T m ,   s a í d a 2 e que nossas resistências são encontradas assim:

R e v ,   e n t r a d a = 1 h _ e n t r a d a   .   A s R e v ,   s a í d a = 1 h _ e v ,   s a í d a   .   A s R r a d = 1 h _ r a d   .   A s

Dessa forma, podemos simplificar ainda nossa equação para o q s a í d a :

q s a í d a = T _ m   -   T _ s R e v ,   e n t r a d a

Passo 6

Agora na letra d, basta a gente encontrar as temperaturas baseado nas equações anteriores, vamos ter que:

T m ,   o = 45,7 ° C T _ s = 34 ° C

Uhul!! Conseguimos!

Resposta

  1. h _ e v ,   o = 4,03   W / m ² . K

  2. h _ r a d = 3,2   W / m ² . K

  3. q s a í d a = T _ m   -   T _ s R e v ,   e n t r a d a

  4. T m ,   o = 45,7 ° C T _ s = 34 ° C
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um recipiente esférico com 30c m de diâmetro externo é utilizado como reator para lenta reação endotérmica. O recipiente está completamente submerso em um grande tanque cheio de água, mantido a
Uma placa de circuito impresso de 12c m de altura e 20c m de largura abriga em sua superfície 100 chips estreitamente espaçados, cada um dissipando 0,05W . A placa é resfriada por um ventilador que so
Em uma fábrica, placas finas e quadradas de 3m × 3m que saem de um forno a 270 ℃ ℃ são refrigeradas soprando-se ar ambiente a 18 ℃ ℃ horizontalmente paralelo às suas superfícies. Determine a velocidad
Uma barra vertical de 150m m de diâmetro e 1c m de comprimento tem água escoando em toda sua superfície externa a uma velocidade de 0,5m / s . A temperatura da água é uniforme a 40 ℃ ℃, e a temperatur
Quando nem a convecção natural nem a forçada são desprezíveis, é correto calcular cada uma de forma independente e adicioná-las para determinar a transferência total de calor por convecção?