Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 9.Problemas - Ex. 71

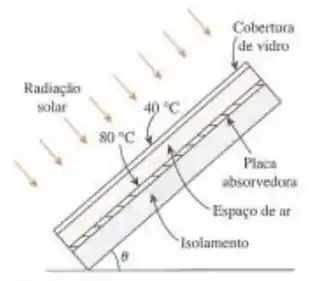
Os coletores solares de placa plana são, muitas vezes, inclinados em direção ao sol, a fim de interceptar maior quantidade de radiação solar direta. O ângulo de inclinação a partir da horizontal também afeta a taxa de perda de calor do coletor. Considere um coletor solar de 1,5 m de altura e 3 m de largura, inclinado em um ângulo θ a partir da horizontal. O verso da placa absorvedora está muito bem isolado. A placa absorvedora e a cobertura de vidro, que são espaçadas 2,5 cm uma da outra, são mantidas a temperaturas de 80°C e 40°C, respectivamente. Determine a taxa de perda de calor da placa absorvedora por convecção natural para θ = 0 ° ,   30 °   e   90 ° .

Passo 1

E vamos continuando as questões por aqui !!

O que nós queremos é a taxa de transferencia de calor por convecção:

Q c o n v ˙ = h A s T 1 - T 2

Como o espaçamento é retangular:

A s = H w

Então:

Q c o n v ˙ = h H w T 1 - T 2

O que nós sabemos?

Sabemos que:

H = 1,5   m

L = 3   m

T 1 = 80 ° C

T 2 = 40 ° C

Então nós precisamos achar o coeficiente de calor convectivo, certo?

Passo 2

O coeficiente é dado por:

h = k N u L c

Sabemos que o comprimento é a espessura:

L c = 2,5   c m = 0,025   m  

Mas ainda precisamos calcular algumas coisas, certo?

Antes de qualquer coisa, o que fazemos?

Acertou quem disse achar a temperatura médiaaa:

T m é d i a = T 1 + T 2 2 = 80 ° C + 40 ° C 2 = 60 ° C

Com isso nós já achamos o coeficiente de expansão volumétrica, né?

β = 1 T m é d i a = 1 60 + 273   K

β = 0,003 003   K - 1

Olhando na Tabela A-15 à 60°C:

k = 0,028 08   W m K

P r = 0,7 202

v T m é d i a = 1 , 896   × 10 - 5 m 2 s

Com isso nós achamos a condutividade térmica, mas nada sobre o número de Nusselt, né?

Para calculá-lo vamos precisar do número Rayleigh, dado por:

R a = g β T 1 - T 2 L ³ v 2 P r

Substituindo:

R a = 9,81 m s 2 0,003003   K - 1 80 ° C - 40 ° C 0,025   m 3 1,896   × 10 - 5 m 2 s 2 0,7202

R a = 36887,63

Passo 3

Bom galera, agora nós temos todos os dados que precisaremos.

Começando pela letra (a) quando o ângulo valo 0° a placa esta na horizontal, certo?

Neste caso o Número de Nusselt é dado por:

N u = 1 + 1,44 1 - 1708 R a + + R a 1 3 18 - 1 +

Onde o sinal + significa que valores negativos serão substituídos por zero. Substituindo:

N u = 1 + 1,44 1 - 1708 36887,63 + + 36887,63 1 3 18 - 1 +

N u = 3,223

Calculando o coeficiente convectivo:

h = 0,02808   W m K 3,223 0,025   m = 3,62 W m 2 K

Agoora sim nós temos tudo o que precisamos para calcular a transferência de calor:

Q c o n v ˙ = 3,62 W m 2 K 1,5   m 3   m 80 ° C - 40 ° C

Q c o n v ˙ = 651,6   W

Passo 4

Quando a inclinação passa para 30° o Número de Nusselt é calculado de forma diferente.

Vamos ver como?

N u = 1 + 1,44 1 - 1708 R a . cos ⁡ θ + + 1 - 1708 . ( sin ⁡ 1,8 θ ) 1.6 R a . cos ⁡ θ + ( R a . cos ⁡ θ ) 1 3 18 - 1 +

Substituímos:

N u = 1 + 1,44 1 - 1708 36887,63 . cos ⁡ 30 ° + + 1 - 1708 . ( sin ⁡ 1,8 × 30 ° ) 1.6 36887,63 . cos ⁡ 30 ° + ( 36887,63 × cos ⁡ 30 ° ) 1 3 18 - 1 +

N u = 3,092

Com o novo Nu obtemos um novo valor para o coeficiente convectivo:

h = 0,02808   W m K 3,092 0,025   m = 3 , 4729 W m 2 K

Agoora sim nós temos tudo o que precisamos para calcular a transferência de calor:

Q c o n v ˙ = 3 , 4729 W m 2 K 1,5   m 3   m 80 ° C - 40 ° C

Q c o n v ˙ = 6 25 , 2   W

Achamos mais uma resposta ein!!

Animados para a última?

Passo 5

No último caso nós temos um ângulo de 90°, ou seja, a placa está na vertical.

Como 10 4 < R a < 10 7 :

N u = 0,42 . R a 0,25 . P r 0,012 H L c - 0,3

Substituindo os dados que já temos:

N u = 0,42 . 36887,63 0,25 . 0,7202 0,012 1,5   m 0,025   m - 0,3

N u = 1,6975

E o novo coeficiente será:

h = 0,02808   W m K 1,6975 0,025   m = 1,9066 W m 2 K

Agoora sim nós temos tudo o que precisamos para calcular a transferência de calor:

Q c o n v ˙ = 1,9066 W m 2 K 1,5   m 3   m 80 ° C - 40 ° C

Q c o n v ˙ = 343,2   W

Ufaaa!!

Grande, mas legal!

Resposta

  1. Q c o n v ˙ = 651,6   W ;
  2. Q c o n v ˙ = 625,2   W ;
  3. Q c o n v ˙ = 343,2   W .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Durante um dia de inverno, a porta de vidro de uma porta balcão externa, com altura de 1,8m e largura de 1,0 m, mostra uma linha de gelo próximo a sua base. A temperatura das paredes da sala e do ar e
Considere uma série de aletas retangulares verticais, que deve ser usada para resfriar um componente eletrônico, montada em ar atmosférico quiescente a T ∞ = 27 ° C . Cada aleta te L = 20 mm e H = 150
27 – Considere as condições do exemplo 9.3, incluído o efeito da adição de um isolamento de espessura t e condutividade térmica k=0,035 W/m.K para o duto. Nós desejamos agora incluir o efeito da radia
85 – Um cilindro horizontal de 25 mm de diâmetro é mantido a uma temperatura uniforme de 35°C. Ar atmosférico com velocidade de 0,10 m/s e temperatura de 20°C está em um fluxo cruzado sobre o cilindro
30 – Um disco de alumínio quente de 0,5 m de diâmetro e 35 mm de espessura é resfriado de uma temperatura inicial Ti=400°C em um grande banho de óleo de temperatura To=35°C. Como está resfriando, o di