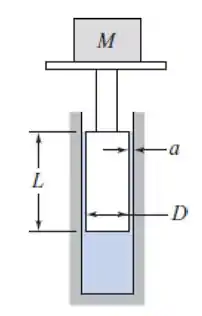
O componente básico de um aparelho de teste de manômetros consiste de um dispositivo pistão-cilindro, conforme mostrado. O pistão, de 6 mm de diâmetro, é carregado de modo a desenvolver uma pressão de módulo conhecido. (O comprimento do pistão é 25 mm.) Calcule a massa, M, requerida para produzir 1,5 MPa (manométrica) no cilindro. Determine a taxa de vazamento como uma função da folga radial, , para essa carga, se o líquido for óleo SAE 30 a 20°C. Especifique a máxima folga radial admissível de modo que o movimento vertical do pistão devido ao vazamento seja inferior a 1 mm/min.

Podemos modelar esse exercício como sendo um escoamento laminar com gradiente de pressão entre placas estacionárias e paralelas, e dessa forma, utilizar a equação 8.6c vista nesse capítulo, então, temos:

De forma que o perímetro será:

Em que é o diâmetro do pistão, então, substituindo essa expressão na equação anterior e isolando a vazão, temos:

Agora precisamos pegar as propriedades do óleo à temperatura dada no enunciado no apêndice A, então, teremos:

Então, agora, substituindo os valores conhecidos na equação da vazão obtida no passo 2, temos:

Agora, para que o movimento do pistão devido ao vazamento seja iferior a 1mm/min. Devemos usar a equação da vazão para descobrir o valor utilizando essa velocidade, então, teremos:

Antes de aplicar a equação, vamos converter a velocidade para , então, temos:

Então, susbtituindo os valores conhecidos na equação da vazão, temos:

Então, voltando à equação do passo 3 para a vazão, e substituindo o valor encontrado, temos: