Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 176

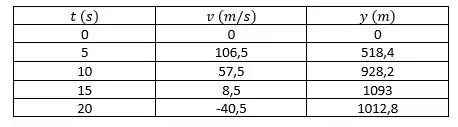
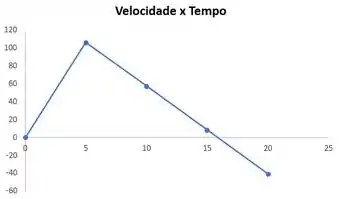
Um modelo de foguete, a propelente sólido, tem uma massa de 69,6   g , da qual 12 ,   5   g são de combustível. O foguete produz 5,75   N de empuxo por um período de 1,7   s . Para essas condições, calcule a velocidade máxima e altura atingida, na ausência de resistência do ar. Trace um gráfico da velocidade do foguete e da distância percorrida como funções do tempo.

Passo 1

Considerações Iniciais:

  1. Escoamento em estado estacionário;
  2. Escoamento incompressível;
  3. Escoamento com velocidade constante;
  4. Escoamento uniforme.
  5. Força de resistência desprezível.

Passo 2

Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:

F = F S + F B - ∫ V C a r ρ d ∀ = ∂ ∂ t ∫ V C V ρ   d ∀ + ∫ S C V ( ρ V ) d A

Como estamos analisando um sistema y , temos:

F S y + F B y - ∫ V C a r y ρ d ∀ = ∂ ∂ t ∫ V C v ρ   d ∀ + ∫ S C v ( ρ V ) d A

Não há resistência:

- m g - ∫ V C a r y ρ d ∀ = ∂ ∂ t ∫ V C v ρ   d ∀ + ∫ S C v ( ρ V ) d A

Não temos a variação das propriedades com o tempo, então:

∂ ∂ t = 0

Assim:

- m g - ∫ V C a r y ρ d ∀ = ∫ S C v ( ρ V ) d A

Então:

- m g - a r y m = - v e ⋅ m ˙

a = v e ⋅ m ˙ m - g  

Sendo:

a r y = d v d t ;

m = m o - m ˙ t .

Temos:

d v d t = v e ⋅ m ˙ m o - m ˙ t - g  

Isolando os termos:

∫ 0 v d v = ∫ 0 t v e ⋅ m ˙ m o - m ˙ t - g   d t

Integrando:

v = - v e ln ⁡ 1 - m ˙ t m 0 - g t

Passo 3

Calculando m ˙ .

m f = m ˙ t

m ˙ = m f t

Sendo:

m f = 12,5   g = 0,0125   k g ;

t = 1,7   s .

Temos:

m ˙ = 0,0125 1,7 = 0,00 735   k g / s

Calculando v e :

F e = v e m ˙

v e = F e m ˙

Sendo:

F e = 5,75   N .

Temos:

v e = 5,75 0,00735 = 782   m / s

Passo 4

Calculando a velocidade máxima.

v m á x = - v e ln ⁡ 1 - m ˙ t m 0 - g t

Sendo:

m 0 = 69,6   g = 0,0696   k g ;

g = 9,8   m / s 2 .

Temos:

v m á x = - 782 ⋅ ln ⁡ 1 - 0,00735 ⋅ 1,7 0,0696 - 9,8 ⋅ 1,7 = 138,8   m / s

Passo 5

Calculando a altura atingida.

Temos que:

v = d y d t

Então:

d y d t = - v e ln ⁡ 1 - m ˙ t m 0 - g t

Integrando:

y = v e m 0 m ˙ 1 + 1 - m ˙ t m 0 ⋅ ln ⁡ 1 - m ˙ t m 0 - 1 - g t 2 2  

Substituindo os dados:

y = 782 ⋅ 0,0696 0,00735 1 + 1 - 0,00735 ⋅ 1,7 0,0696 ⋅ ln ⁡ 1 - 0,00735 ⋅ 1,7 0,0696 - 1 - 9,8 ⋅ 1,7 2 2

y = 113,7   m

Passo 6

v t = v m á x - g ( t x - t )

y t = y + v m á x t x - t - g t x - t 2 2

Resposta

v m á x = 138,8   m / s

y = 113,7   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma fresta estreita entre duas placas circulares está inicialmente preenchida com líquido incompressível. Em t = 0 , a placa superior, inicialmente distate h 0 da placa inferior, começa a mover-se par
A água de um jato de diâmetro D é usada para suportar o objeto cônico mostrado. Deduza uma expressão para a massa combinada do cone e da água, M , que pode ser suportada pelo jato, em termos de parâme
No antigo Egito, vasos circulares cheios de água eram por vezes utilizados como relógios primitivos. Os vasos tinham um formato tal que, à medida que a água drenava pelo fundo, o nível da superfície d
Um fluido incompressível de viscosidade desprezível é bombeado com uma vazão volumétrica total Q por uma superfície porosa para o interior de uma pequena fresta entre placas paralelas estreitamente es
Uma corrente de fluido incompressível movendo-se a baixa velocidade sai de um bocal apontado diretamente para baixo. Considere que a velocidade em qualquer seção reta seja uniforme e despreze efeitos