Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 99

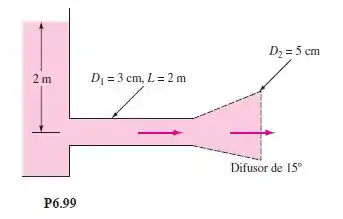
Na Seção 6.11, mencionou-se que os usuários do aqueduto de Roma obtinham água adicional acoplando um difusor nas saídas de seus tubos. A Figura P6.99 ilustra uma simulação: um tubo liso de entrada, com ou sem um difusor cônico de 15 ° expandindo para uma saída de 5 cm de diâmetro. A entrada do tubo é canto vivo. Calcule a vazão volumétrica (a) sem o difusor e (b) com o difusor.

Passo 1

Bora pra mais uma!

Para a água a 20 °   temos que ρ = 998 k g m 3   e   μ = 1,002 * 10 - 3 N s m 2 .   Da equação da energia aplicada entre a superfície do aqueduto e a saída do tubo, temos:

z s u p e r f i c i e = z 2 + V 2 2 2 g + h p + ∑ h m = z 2 + V 2 2 2 g + V 1 2 2 g ( f L D 1 + K e n t r a d a + K d i f u s o r )

  1. Sem o difusor, temos que K d i f u s o r = 0 e V 1 = V 2 , então, sendo K e n t r a d a = 0,5 , obtemos:

    2. 2 m = V 1 2 2 * 9,8 m s 2 f * 2 m 0,03 m + 1 + 0,5

    Vamos supor um chute de f = 0,02

    Daí:

    V 1 = 3,72 m s → R e = 998 k g m 3 1,002 * 10 - 3 N s m 2 * 3,72 m s * 0,03 m = 111154,5

    Obtemos então um novo fator de atrito para tubo liso:

    f t u b o l i s o R e = 0,0175  

    Agora, vamos novamente iterar:

    V 1 = 4,47 m s → R e = 998 k g m 3 1,002 * 10 - 3 N s m 2 * 4,47 m s * 0,03 m = 1 15000

    O novo f permanece 0,0175, ou seja, nosso processo iterativo convergiu!

    Agora, a vazão volumétrica será:

    Q = V A s a i d a = 4,47 m s * π * 0,015 m 2 = 0,00 32 m 3 s .

    Passo 2

  2. Agora, com o difusor, temos que D 1 D 2 = 0,6   e 2 θ = 15 ° , da figura 6.23 do livro, obtemos K d i f u s o r ≈ 0,2 . Da equação da continuidade:

V 1 A 1 = V 2 A 2 → V 2 = 3 5 2 V 1 = 0,36 V 1

Retornando à equação da energia, temos:

2 m = 0,36 V 1 2 2 g + V 1 2 2 g 1 + 0,5 + f * 2 m 0,03 m + 0,2

Vamos novamente fazer um processo iterativo, fazendo o mesmo chute f = 0,02 . Com apenas duas iterações (idênticas as feitas no item a), obtemos que f   converge para 0,017.

Daí:

0,36 V 1 2 2 * 9,8 m / s ² + V 1 2 2 * 9,8 m / s ² 1 + 0,5 + 0,017 * 2 m 0,03 m + 0,2 = 2 m

V 1 = 3,64 m s .

Q = V A s a i d a = 3 , 64 m s * π * 0,015 m 2 = 0,002 6 m ³ s

Resposta

  1. 0,0032 m 3 s
  2. 0,0026 m ³ s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um macaco hidráulico suporta uma carga de 50.000 N/m por pé de comprimento perpendicular ao diagrama. O mancal é alimentado com óleo SAE 10W – 30 a 35°C e 700 kPa através do rasgo central. Como o óleo
O perfil de velocidade para escoamento completamente desenvolvido entre placas planas paralelas estacionadas é dado por u = a ( h 2 / 4 - y 2 ) , na qual a é constante, h é o espaçamento entre as plac
Água a 60 ° C escoa para a direita entre duas grandes placas planas. A placa inferior se move para a esquerda com velocidade de 0,3m / s ; a placa superior está parada. O espaçamento entre as placas é
Usando o perfil do Problema 8.18, mostre que a vazão obtida a partir da lei de potência para escoamento laminar, completamente desenvolvido, de um fluido entre placas planas paralelas pode ser escrita
Considere o escoamento laminar completamente desenvolvido entre placas paralelas infinitas espaçadas de d=10m m . A placa superior se move para a direita com velocidade U 2=0,5m / s ; a placa inferior