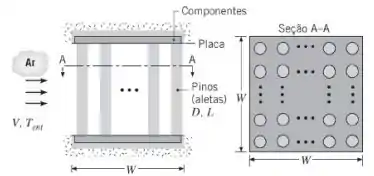
Componentes elétricos montados sobre duas placas isotérmicas são resfriados pela passagem de ar atmosférico entre as placas. Uma configuração alinhada de pinos de alumínio entre as placas é usada para aumentar a transferência de calor para o ar. Os pinos possuem diâmetro , comprimento e condutividade térmica Os passos longitudinal e transversal são , formando uma matriz quadrada com pinos As placas são quadradas e possuem, cada uma, de lado. O ar entra na matriz de pinos com uma velocidade de e uma temperatura de.

(a) Avaliando as propriedades do ar a estime o coeficiente convectivo médio na matriz de pinos.

(b) Admitindo um coeficiente convectivo uniforme em todas as superfícies de transferência de calor (placas e pinos), use o resultado da parte (a) para determinar a temperatura do ar na saída do sistema e a taxa de transferência de calor total, quando as placas são mantidas a . Sugestão: A temperatura de saída do ar é governada por uma relação exponencial que possui a forma sendo a vazão mássica de ar atravessando a matriz de pinos, a área superficial total para a transferência de calor (placas e pinos), e a eficiência global da superfície, como definida pela Equação 3.107.

Para resolver essa questão vamos assumir que:

(1) Estamos em condição de estado estacionário;

(2) A radiação é desprezível;

(3) A condução é unidimensional nos pinos;

(4) A temperatura é uniforme da placa;

(5) As placas têm um efeito insignificante no fluxo sobre os pinos;

(6) O coeficiente de convecção é uniforme sobre todas as superfícies, correspondendo ao coeficiente médio do fluxo sobre um feixe de tubos.

Da relação Zukauskas temos:

Com,

Da Tabela 7.5, temos que:

e

Então,

Se for considerado a temperatura de todas as superfícies de transferência de calor, deve-se fazer a correção da queda de temperatura real ao longo dos pinos. Isso é feito através da introdução da eficiência geral da superfície e da substituição de por . Portanto, para obter a temperatura da saída de ar, temos:

Onde,

Substituindo os valores, temos que:

Além disso,

Com simetria sobre o plano médio do pino,

Então,

Com , temos:

Substituindo os valores, temos que:

Então,

Com simetria sobre o plano médio do pino,

A taxa de calor total é,