Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 24
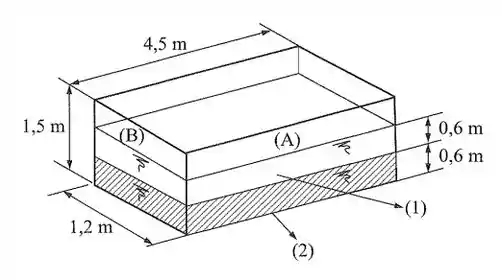
Um tanque retangular, como da figura, tem de comprimento, de largura e de altura. Contém de água e de óleo. Calcular a força devida aos líquidos nas paredes laterais e no fundo. Dados:
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Essa é uma questão que exige bastante atenção nas continhas pois sabemos que a distribuição de pressão nas paredes vai mudar pois o fluido não é o mesmo ao longo da parede.
A distribuição de pressão vai se comportar da seguinte maneira:
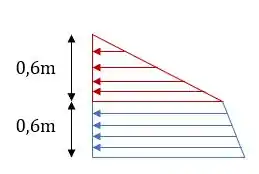
Podemos calcular as pressões nas bases de cada fluido:
Para o fluido temos que:
Logo:
Passo 2
Temos então o seguinte arranjo:
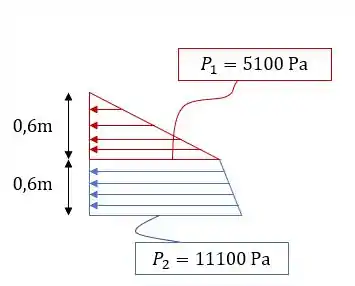
De acordo com a teoria o volume do prisma de pressão é a força exercida na parede. Logo, observando o aspecto geométrico é de:
O Volume do fluido é dado por um prisma triangular, logo:
Aplicando ao problema, temos que:
O Volume do fluido é dado por um prisma trapezoidal, logo:
Aplicando ao problema, temos que:
Passo 3
A força resultante será então:
Como cada parede tem a sua determinada largura, para a parede , temos que:
E para a parede , temos que:
Substituindo pelos valores, temos que:
E:
Passo 4
A força exercida no fundo é dada pela soma dos pesos dos fluidos. Portanto:
O volume de água dos dois fluidos é o mesmo, portanto:
Resolvendo, temos que: