Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 78

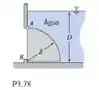
Uma comporta, na forma de um quarto de cilindro, articulada em A e vedada em B, tem 3 m de largura. O fundo da comporta está 4,5 m abaixo da superfície da água. Determine a força sobre o batente B, se a comporta for feita de concreto; R = 3 m.

Passo 1

Nessa questão temos a geometria da porta. Vamos encontrar a força no batente B .

Para resolução, aplicaremos as equações hidrostáticas a seguir:

d p d h = ρ g , pressão hidrostática

∑ M = 0 , equilíbrio de rotação

F v = ∫ p d A y , força hidrostática vertical

x ' F v = ∫ x d F v , momento de força vertical

y ' F H = ∫ y d F H , momento de força horizontal

Como todo problema da MecFlu, fazemos as seguintes considerações: fluido estático; densidade constante; pressão atmosférica do outro lado.

Precisamos calcular a força devido à água na superfície curva e por baixo. Assim, temos o seguinte desenho:

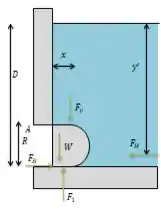
Para superfícies curvas, podemos integrar a pressão, mas aqui usamos os conceitos de que F v é equivalente ao peso do fluido acima e F H é equivalente à força sobre uma placa plana vertical.

Passo 2

Para F v temos:

F v = W 1 - W 2

Logo,

W 1 = ρ g w D R = 1000 k g m 3 × 9,81 m s 2 × 3 m × 4,5   m × 3 m = 397   k N

W 2 = ρ g w π R 2 4 = 1000 k g m 3 × 9,81 m s 2 × 3 m × π 4 × 3 m 2 = 208   k N

F v = 189   k N

Com x que será:

F v x = W 1 R 2 - W 2 4 R 3 π

x = 397 189 × 3 2 - 208 189 × 4 × 3 3 π = 1,75   m

Passo 3

Agora para a força horizontal, temos:

F H = p c A = ρ g D - R 2 w R

F H = 1000 k g m 3 × 9,81 m s 2 × 4,5 - 3 2 3   m × 3 m = 265 k N

Assim, a localização da força é:

y ' = y c + I x x A y c

y ' = D - R 2 + w R 3 12 × 1 w R D - R 2

y ' = D - R 2 + R 2 12 D - R 2

y ' = 4,5 - 3 2 + 3 2 12 4,5 - 3 2

y ' = 3,25   m

A força F 1 no fundo do portão é:

F 1 = p A = ρ g   D w R

F 1 = 1000 k g m 3 × 9,81 × 4,5 × 3 × 3 = 397   k N

Para o portão de concreto:

W c o n c r e t o = S G ρ g w π R 2 4 = 2,4 × 1000 k g m 3 × 9,81 m s 2 × 3   m × π ( 3 ) 2 4

W c o n c r e t o = 499   k N

Então a força sobre o batente será:

F B R + F 1 R 2 - W c o n c r e t o 4 R 3 π - F v x - F H y ' - D - R = 0

F B = 4 3 π   W c o n c r e t o + x R F v + y ' - D - R R × F H - 1 2 × F 1

F B = 4 3 π × 499   k N + 1,75 3 × 189   k N + 3,25   - 4,5 - 3 3 × 265 k N - 1 2 × 397   k N

F B = 278   k N

Resposta

F B = 278   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O pórtico circular de acesso na lateral de um reservatório vertical de água tem diâmetro de 0,6 m e está fixado por oito parafusos igualmente espaçados em torno da circunferência. se o diâmetro da col
A comporta AOC mostrada na figura tem 1,8 m de largura e é articulada em O. Desconsiderando o peso da comporta, determine a força na barra AB. A comporta é vedada em C.
A comporta retangular mostrada na figura abrese automaticamente, quando o nível da água no seu lado esquerdo atinge uma determinada altura. A que profundidade acima da articulação isto acontece? Despr
Para a geometria mostrada, qual é a força vertical sobre a represa? Os degraus têm 0,5 m de altura, 0,5 de profundidade e 3 m de largura.
Para a geometria mostrada, qual é a força vertical da água sobre a represa?