Enunciado
Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 64
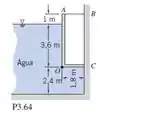
A comporta AOC mostrada na figura tem 1,8 m de largura e é articulada em O. Desconsiderando o peso da comporta, determine a força na barra AB. A comporta é vedada em C.
Passo 1
Temos nessa questão o portão , articulado ao longo de , possui largura conhecida; o peso do portão pode ser negligenciado. O objetivo é determinar a força na barra , para isso, aplica-se as equações hidrostáticas neste sistema, sendo elas
, referente a pressão hidrostática ( é positivo para baixo)
, equilíbrio rotacional
, força hidrostática
, a localização da linha de ação
Fazemos algumas considerações: fluido estático; fluido incompressível; a pressão atmosférica atua na superfície livre da água e fora do portão; não há momento de resistência na dobradiça em ; não há resistência vertical em .
O diagrama que representa esse sistema é o seguinte:
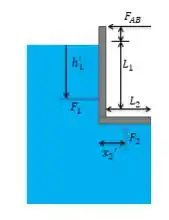
Como podemos perceber, é o resultado da força distribuída em ; é a resultante da força distribuída em ; é a força da barra e é a força de vedação em .
Passo 2
Para resolvermos, encontramos a força em , que é a
Substituímos os dados e temos:
Agora, precisamos calcular a linha de ação referente a :
Assim, calculando, temos
Passo 3
Da mesma forma do passo 3, fazemos para a força do lado ,
Pelo fato da pressão ser uniforme sobre o plano , temos que a linha de força atuando no centro é , aproximadamente a metade do comprimento .
Passo 4
Feito todas essas analises podemos avaliar as forças (tendo cuidado com os sinais),
Isolamos, então
Prontinho!!