Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 78

Mostre que o coeficiente de energia cinética, α , para o perfil de velocidade turbulenta da "lei de potência” da Eq. 8.22 é dado pela Eq. 8.27. Trace α como uma função de R e , para R e   =   1   ×   10 4   a   1   ×   10 7 . Na análise de problemas de escoamento no interior de tubos é prática comum considerar α   ≈   1 . Trace um gráfico do erro associado a esta consideração como uma função de R e , para R e   =   1   ×   10 4   a   1   ×   10 7 .

Passo 1

Fala aí galera, vamos para mais um problema de Mecânica dos fluidos. A equação 8.26b é:

α = ∫ ρ V 3 d A m t a x a V m é d ²

Onde V é a velocidade, m t a x a é a taxa de fluxo de massa e V m é d é a velocidade média.

Para o perfil da lei de potência (Eq. 8.22):

V = U 1 - r R 1 n

Para a taxa de fluxo de massa:

m t a x a = ρ π R 2 V m é d

Logo, o denominador da equação 8.26b será:

m t a x a V m é d 2 = ρ π R 2 V m é d 3

Em seguida, devemos avaliar o numerador da Eq. 8.26b:

∫ ρ V 3 d A = ∫ ρ 2 π r U 3 1 - r R 3 n d r

∫ 0 R ρ 2 π r U 3 1 - r R 3 n d r = 2 π ρ R 2 n 2 U 3 3 + n 3 + 2 n

Qualquer dúvida sobre como resolvemos esta integral, é só dar uma olhada na parte de integrais no Responde aí, passei rápido por ela porque não é nosso foco.

Passo 2

Agora, temos o numerador e denominador da equação 8.26b:

α = ∫ ρ V 3 d A m t a x a V m é d 2 = 2 π ρ R 2 n 2 U 3 3 + n 3 + 2 n ρ π R 2 V m é d 3

Logo:

α = U V m é d 3 2 n 2 3 + n 3 + 2 n

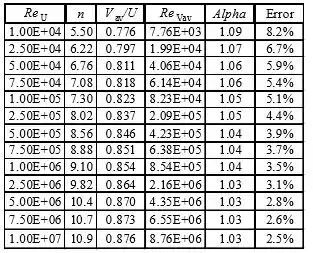
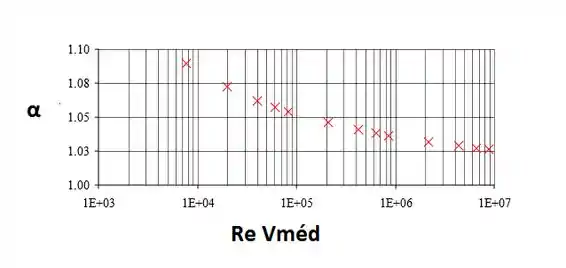
Para plotar α versus R e V m é d , usamos as seguintes relações paramétricas:

n = - 1,7 + 1,8 log ⁡ R e u → E q   8.23

V m é d U = 2 n 2 n + 1 2 n + 1 → E q   8.24

R e V m é d = V m é d U R e U

α = U V m é d 3 2 n 2 3 + n 3 + 2 n

Um valor de R e U leva a um valor para n ; isso leva a um valor para V m é d U ; estes levam a um valor para R e V m é d e α .

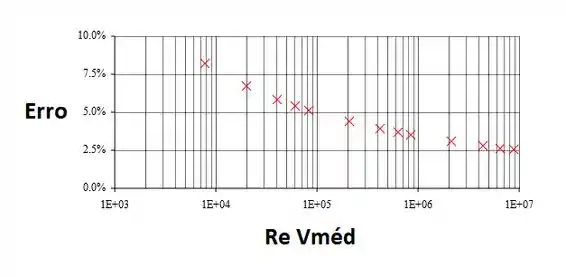
Os gráficos de α e o erro ao assumir α   =   1 , versus R e V m é d , podem ser feitos no Excel.

Passo 3

Plotando os gráficos com a ajuda do Excel:

Resposta

α = 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Numa fábrica constrói-se um trocador de calor, cujos diâmetros de entrada e saída são 10c m . Para determinar o comprimento equivalente do trocador, constrói-se o circuito da figura, no qual todas as
Uma grande massa é suportada por um pistão de diâmetro D = 100m m e comprimento L = 100m m . O pistão está assentado em um cilindro fechado no fundo. A folga a = 0,025m m entre a parede do cilindro e
Uma alta pressão em um sistema é criada por um pequeno conjunto pistão-cilindro. O diâmetro do pistão é 6 mm e ele penetra 50 mm no cilindro. A folga radial entre o pistão e o cilindro é 0,002 mm. Des
Um macaco hidráulico suporta uma carga de 9000 kg. Os seguintes dados estão disponíveis:Diâmetro do pistão: 100 mmFolga radial entre o pistão e o cilindro: 0,05 mmComprimento do pistão: 120 mmEstime a
Um óleo viscoso escoa em regime permanente entre duas placas paralelas estacionárias. O escoamento é laminar e completamente desenvolvido. O espaçamento entre as placas é h = 5m m . A viscosidade do ó