Enunciado
Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 63
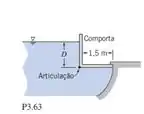
A comporta retangular mostrada na figura abrese automaticamente, quando o nível da água no seu lado esquerdo atinge uma determinada altura. A que profundidade acima da articulação isto acontece? Despreze a massa da comporta.
Passo 1
Nesse problema temos um portão com geometria retangular e deve-se encontrar a profundidade para o portão abrir.
Sistematizando o problema, demonstrando as forças que atuam, temos
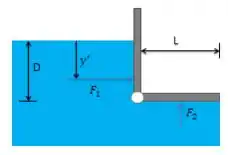
Assim as equações a serem tomadas como base são:
, referente a pressão hidrostática ( é positivo para baixo)
, o somatório do momento na direção
, força hidrostática
, a localização da linha de ação
E, por fim, fazemos algumas considerações: Fluido estático; densidade constante; pressão atmosférica do outro lado; sem atrito na dobradiça.
Passo 2
Para fluido incompressível , em que é a pressão manométrica a altura é medida para baixo.
A força no portão vertical (portão 1) é a mesma que em um retângulo de tamanho e largura . Logo,
A localização da linha de ação,
A força no portão horizontal (portão 2) é devida à pressão constante e está no centroide.
Calculando o momento sobre a dobradiça, temos
Agora, substituímos
Assim,